atuzlak | Data Analysis Cheatsheet

Feel free to contact me if you have any questions, suggestions, feedback, or would like to help me change the website such that formulae are displayed correctly (MathJax) and code-snippets are highlighted (highlight.js).
For the lab courses I highly recommend using the GitHub Copilot extension

This website in Jupyter-Notebook
Python Library and corresponding Documentation+Workspace for the exam

Week 1
Week 2
Week 3
Week 4
Week 5
Week 6
Week 7
Week 8
Week 9
Week 10
Week 11
Week 12
Week 13
Week 14
Week 15
WoF

Library , Beispiel , Wichtig , Highlighted, Bemerkung

Week 1 #

Basics, Arrays / Numpy-Arrays, Laden und Speichern von Daten

import numpy as np

np.array? öffnet documentation
Bsp :
a = np.array([1, 2, 3]) , np.zeros(n) , np.ones(n) , np.ones(n, dtype=int oder float) ,
a *= 2 👉 [2, 4, 6] , a[-1] 👉 6 letztes El.
b = np.array([[1, 2, 3], [97, 98, 99]])
a.shape 👉 Dimension (Zeilen, Spalten)

a[i_start : i_stop : i_step] (falls a[::] 👉 i_start = 0, stop = "array.length", step = 1)
a[i_start : i_stop] indexierung bei n-dim. (hier 2-D) Arrays : b[1, 0:] 👉 [97, 98, 99] Operationen auf Teilbereichen ebenfalls möglich

print?
Bsp :
print(a, end=';') 👉 [2, 4, 6]; falls loop durch array dann 2;4;6;
print('x = {}'.format(7)) {:d} (int), {:f} (float), {:0.nf} (float mit n nachkommastellen) 👉 x = 7

Loops
Bsp :
for index, value in enumerate(a):
a[index] = val**2
a 👉 [4, 16, 36]

for i in range(i_start, i_end, i_step):
for i in a[1:]:

import os

Navigation
Bsp :
cwd = os.getcwd() , os.listdir(cwd) 👉 ['file1', 'file2', ...] , file = os.path.join(cwd, 'filename') , os.chdir(r"path")
files = os.listdir()
index = files.index('filename')
👉 data = np.loadtxt(files[index] , dtype=float, comments='#', ...)

Speichern / Lesen
Bsp :
data = np.loadtxt(file, dtype='float', comments='#', delimiter=',' , skiprows=n ) falls Dataset-dimension und Anzahl Zeilen z.B. 2 ist geht auch x, y = np.loadtxt(...)
z.B.: print(data) 👉 [7, 7, 7, 420, 69]

np.savetxt('filename', (x, y, z) arrays oder variablen , delimiter=',', header='Beispieldatei Datenanalyse, 14.02.2023. Format: x, y, z') (x, y, z ➡️ np.array([...]))

..."low-level" :
with open('filename', 'r') as f:
lines = f.readlines()

with open('filename', 'w') as f:
f.writelines('x, y, z\n')
for i in range(0, len(x)):
f.writelines('{:0.5f}, {:0.5f}, {:0.5f}\n'.format(x[i], y[i], z[i]))

Additional Stuff
np.sum , np.empty (faster than np.zeros) , np.arange(a_min, a_max, distance_from_points) , np.linspace(a_min, a_max, amount_of_points) , len(a) , np.fromstring , np.append, np.transpose

Week 2 #

Funktionen, Mittelwert / Standardabweichung, Histogramm, Normalverteilung

Funktionen
def function_name(parameter1, parameter2, keyword_argument=initial_value):
...
return return_value1, return_value2

❗️ ACHTUNG : Funktionsname nicht als Variablenname brauchen ❗️

import matplotlib.pyplot plt

plt.plot?
plt.plot(x, y) x.shape == y.shape , plt.figure , plt.show , plt.title , plt.xlabel , plt.ylabel , plt.grid , plt.subplot(row, column, index) multiple plots in one fig. color attribute : color = 'color' or 'hex' , plt.bar , plt.barh horizontal , plt.hist
Bsp :
fig = plt.figure()
a = fig.add_subplot(1, 1, 1)
a.plot(t, V)
a.set_xlabel('t (s)')
a.set_ylabel('V (U)')
a.set_title('Rauschen einer Messung')

np.histogram?
np.histogram(V, bins)
Bsp :
cm = 1 / 2.54 Umrechnung Zoll zu Centimeter
binsize = 0.01
bins = np.arange(np.min(V), np.max(V), binsize)
hist, _ = np.histogram(V, bins)
fig = plt.figure(figsize=(30*cm, 25.5*cm))
ax1 = fig.add_subplot(2,2,1)
ax1.bar(bins[:-1], hist, width=0.8*binsize) width < binsize
ax1.set_title('Binsize: {:.2f}V'.format(binsize))

Standardabw. σ = np.sqrt((1/(len(array)-1)) * (1/(len(array))) * np.sum(array)) Mittelwert
np.std 1/n anstatt 1/(n-1) (Approximation für grosse Datensätze)
= np.sqrt(np.var)

Additional Stuff
np.random.rand, np.random.randint(x, size=y) , np.mean , plt.suptitle , plt.scatter , plt.legend
colors = np.array([0, 10, ... , 100]) , plt.scatter(x, y, c=colors, cmap='viridis') colormap , plt.colorbar
np.min , np.max
ax.axvline(Mittelwert, color='r') , ax.set_xlim(13, 16) Zoom in x-Achse 13-16
Normal distribution , Standard deviation , Variance
Zentraler Grenzwertsatz (3blue1brown)

Week 3 #

Auflösung (des Signalwerts) einer Messung, Oszillierendes Signal & Samplingrate

Week 4 #

Fehler des Mittelwertes (mit Gauss), Gausssche Fehlerfortpflanzung

Week 5 #

Kovarianz, Autokovarianz f(t), Korrelationskoeffizient

Kovarianz (σₓᵧ)² = cov(x, y) = (1/(N - 1)) * Σₙ ₌ ₁ᴺ(xₙ - x̄)*(yₙ - ȳ) , [(σₓᵧ)²] = [x] × [y]
np.cov(x, y) 👉 [[(σₓₓ)², (σₓᵧ)²], [(σᵧₓ)², (σᵧᵧ)²]]

(normalisierter) Korrelationskoeffizient ρₓᵧ = (σₓᵧ)²/σₓσᵧ ∈ [-1, 1]
= 0 👉 unkorrelierte Variablen
= ±1 👉 maximal (anti-)korrelierte Variablen
np.corrcoef(x, y) 👉 [[ρₓₓ =1, ρₓᵧ], [ρᵧₓ, ρᵧᵧ =1]]

Autokovarianz
Rₓₓ(Δ) = (1/(N - 1)) * Σₙ ₌ ₁ᴺ(xₙ - x̄)*(xₙ₊Δ - x̄) Indexverschiebung
Rₓₓ(𝜏) = (1/(N - 1)) * Σₜ ₌ ₜ₁ᵗᴺ(x(t) - x̄)*(x(t + 𝜏) - x̄) Zeitverschiebung
Bsp:
Autokovarianzfunktion (fast):

def autocov(x, shift):
if shift == 0:
acov = np.var(x)
else:
N = len(x)
x_mean = np.mean(x)
x_residue = x - x_mean
acov = np.sum(x_residue[:-shift] * x_residue[shift:]) / (N - shift)
return acov

𝜏 → ∞ 👉 Rₓₓ(𝜏) ≈ 0
Korrelationszeit 𝜏꜀ 👉 Rₓₓ(𝜏꜀) ≈ 0

Autokorrelationskoeffizient
ρₓₓ = Rₓₓ(𝜏)/σₓ² ∈ [-1, 1]

Additional Stuff
σₓ = np.sqrt((σₓₓ)²)
plt.tight_layout() keine Überlappung
Bestimmung der Dauer eines kurzen Laserpulses 👉 Autokovarianz oder Autokorrelation, da z.B Laserpulse (z.B 150fs) kürzer als Abtastraten von Detektoren (z.B bis zu 1ns)
Covariance
Autocovariance

Week 6 #

Fouriertransformation (Discrete Fourier Transform DFT), Spektrale Leistungsdichte (Power Spectral Density PSD)

import math

Nyquist-Frequenz fₘₐₓ die ohne Aliasing Effekt gesampled werden kann
fₘₐₓ = 1/2Δt
= 1 / (2 * (t[1] - t[0]))

Frequenzauflösung
Δf = 2*fₘₐₓ/N
= 1 / t[-1] - t[0] oft t[0] = 0

Fourier Transformation
X(fₙ) = (1/N) * Σₖ ₌ ₀ᴺ ⁻ ¹x(tₖ) * exp(-i2πfₙtₖ)
fₙ = nΔf
Δf = 1 / tₜₒₜ
tₖ = kΔt

np.fft.fftfreq(len(array), Δt), np.fft.fft(array)

Bsp:
A = np.fft.fft(array)
A[0] zero-frequency term (the sum of the signal), which is always purely real for real inputs
A[1:math.floor(len(array)/2)] positive-frequency terms
A[math.floor((len(V) / 2) + 1):] negative-frequency terms, in order of decreasingly negative frequency
AmaxEven = A[len(array)/2] represents both positive and negative Nyquist frequency, and is also purely real for real input
AmaxOddPos = A[math.floor((len(V) - 1) / 2)] contains the largest positive frequency
AmaxOddNeg = A[math.floor((len(V) + 1) / 2)] contains the largest negative frequency

f = np.fft.fftfreq(len(array), t[1] - t[0])
spectrum = np.fft.fft(array)
psd = (t[1] - t[0]/len(array)) * np.abs(spectrum)**2

Rücktrafo:
f = np.fft.ifft(spectrum)
real part: np.real(f), imaginary part: np.imag(f)

PSD
Sₓₓ(fₙ) = Δt * |X(fₙ)|² Normierung mit Δt 👉 PSD, sonst PD
👉 wie viel Oszillationsenergie in einem bestimmten Teil des Spektrums vorhanden ist

[Sₓₓ(fₙ)] = Signal²/Frequenz(Hz)
plt.plot(f)(Index, Frequenz), plt.plot(f, psd)(Frequenz, psd)

Additional Stuff
Fourier Transformation (3blue1brown)
PSD
Nyquist-Frequenz

Week 7 #

Rauschen (in PSD), Parseval-Theorem, Glätten, gleitender Mittelwert, Filtern

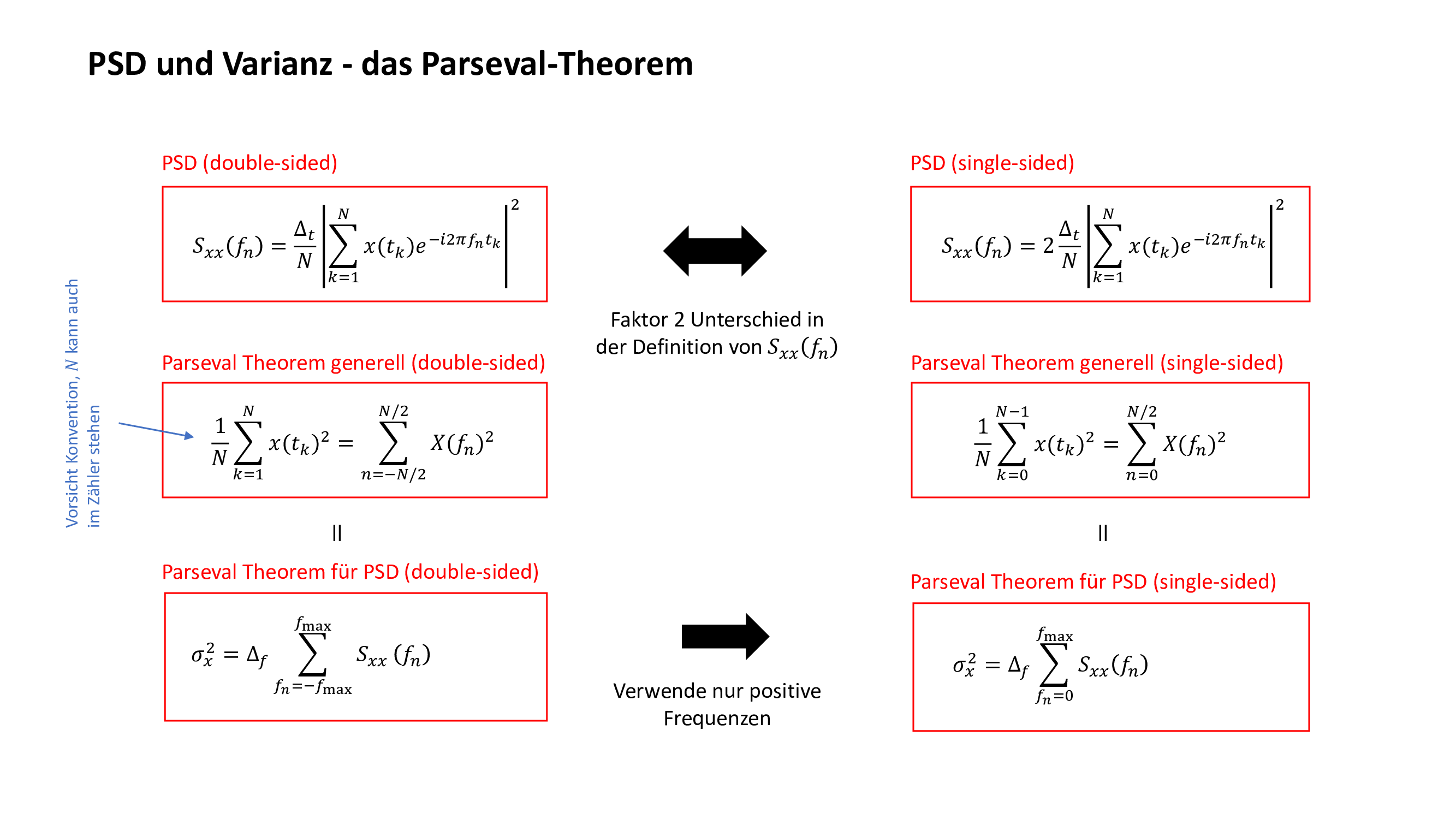
PSDs und Varianzen unkorrelierter Variablen sind additiv:
Sₓₓ(fₙ) = Sₐₐ(fₙ) + S₆₆(fₙ)
σₓ² = σₐ² + σ₆² (Parseval)
folgt aus Substitution 👉 x(tₖ) = a(tₖ) + b(tₖ)

Gleitender Mittelwert 𝑥̃ᵢ = mean({𝑥ᵢ−Δ,...,𝑥ᵢ+Δ})

Filtern im Zeitraum
Bsp:
Glättungsfunktion (mit gleitendem Mittelwert 𝑥̃ᵢ):
#pre: 1-dimensional array, delta is a natural number
#post: delta > 0 👉 smoothened array, delta = 0 👉 copy of array
def smooth(array, delta):
sArray = np.empty(len(array))
for i, val1 in enumerate(array):
if i - delta >= 0 and i + delta < len(array - 1):
s = 0
for j in array[i - delta: i + (delta + 1)]:
s = s + j
sArray[i] = s / ((2*delta) + 1)
else:
sArray[i] = 0

return sArray

Effekt: Schnelles Rauschen wird entfernt, langsame Ausschläge werden beibehalten.
Je grösser delta ist desto glatter wird das Signal, falls aber delta zu gross (abhängig von Datensatz) gewählt wird werden die peaks verbreitert.

Filtern in Frequenzraum
Bsp:
Filterfunktion:
#pre: time axis t, signal, minimum and maximum frequency fMin, fMax
#post: filtered signal (in time domain) 👉 Frequenzen ausserhalb von [fMin, fMax] wurden auf 0 gesetzt
def freqFilter(t, signal, fMin, fMax):
f = np.fft.fftfreq(len(signal), t[1] - t[0])
spectrum = np.fft.fft(signal)
for i in range(len(f)):
if abs(f[i]) < fMin or abs(f[i]) > fMax:
spectrum[i] = 0
filteredf = np.real(np.fft.ifft(spectrum))

return filteredf

Je nach Wahl von fMin und fMax (abhängig von Datensatz), kann man von einem Tief-/Hochpassfilter oder sogar Bandpassfilter sprechen
Tiefpassfilter 👉 kann Einhüllende des Pulses extrahieren (bis auf einen Skalierungsfaktor), dann diese weiter analysieren um z.B. Pulslänge zu bestimmen (z.B. Annäherung durch Gaussfunktion od. numerische ermittlung von FWHM (Week 10))

Additional Stuff
Michelson Interferometer
Parseval Theorem
Gleitender Mittelwert (Moving average)

Week 8 "🏖️" #

Week 9 # (Bayesian Statistics ausgelassen)

Bayesian/Frequentist approach, Wahrscheinlichkeitsverteilung (Charakteristika, Momente), Probability Mass/Density Function (PMF/PDF)

Satz von Bayes
P(B|A) = P(A|B)P(B)/P(A)

Probability Mass Function
Aᵢ diskreter Satz von Ereignissen dann gilt:
P(Aᵢ) ≥ 0
ΣᵢP(Aᵢ) = 1
Bsp:
def PMF(data, resolution):
# Definieren der Bins und Berechnen des Histogramms
# Wir addieren resolution / 1000 zur Obergrenze, um sicherzustellen, dass der letzte Wert auch im Array ist.
bin_centers = np.arange(np.min(data), np.max(data) + resolution / 1000, resolution)
bin_edges = np.linspace(bin_centers[0] - resolution / 2, bin_centers[-1] + resolution / 2, len(bin_centers) + 1)

hist, _ = np.histogram(data, bin_edges)

# Normieren
px = hist / np.sum(hist)

return bin_centers, px
bin_centers 👉 Werte(Signal), px 👉 PMF

Probability Density Function
Falls das Ergebnis des Experiments eine kontinuierliche Zufallsvariable x ist dann gilt:
f(x) ≥ 0
-∞→∞∫f(x)dx = 1
P(a ≤ x ≤ b) = ∫ₐᵇf(x)dx
❗️ Achtung: f(x) ist nicht die Wahrscheinlichkeit, dass x auftritt und [P(Aᵢ)] ≠ [f(x)] ❗️

folgende Formulierungen gelten für PMF und PDF (∫ ↔ Σ), sind jedoch nicht für jede Verteilung sinnvoll

Mode
xₘₒ𝒹ₑ := {x ∈ ℝ : f(x) = max(f(x))}
Für PDF mit nur einem Maximum 👉 xₘₒ𝒹ₑ = df(xₘₒ𝒹ₑ)/dx = 0
Bsp:
def mode(data, res):
x, px = PMF(data, res)
return x[np.argmax(px)]

Median"die Mitte der PDF"
1/2 = -∞→xₘₑ𝒹ᵢₐₙ∫f(x)dx
Bsp:
def median(data, resolution):
x, px = PMF(data, resolution)
# Wir summieren die Wahrscheinlichkeiten auf, bis wir 50% erreicht haben, der Median entspricht
# dem Wert bei 50%.

curr_sum = 0
for i in range(len(x)):
curr_sum += px[i]
if curr_sum >= 0.5:
break

return x[i]

Full Width at Half Maximum (FWHM)
f(a) = f(b) = 1/2f(xₘₒ𝒹ₑ)
FWHM = b - a
FWHMGₐᵤₛₛ = 2σsqrt(2log2)
bei bimodaler Verteilung weniger sinnvoll...
Bsp:
def FWHM(x, y):
# np.where findet alle Werte die die gegebene Bedingung erfüllen und gibt deren Indizes aus.
# Wir wählen also den ersten und letzten Wert der grösser ist als die hälfte des Maximums,
# und geben deren Abstand wieder.
x0 = x[np.where(px >= np.max(y)/2)[0][0]]
x1 = x[np.where(px >= np.max(y)/2)[0][-1]]
return abs(x1 - x0)

Momente
Mₘ := -∞→∞∫xᵐf(x)dx m-te Moment einer PDF
M̃ₘ = 〈(x - M₁)ᵐ〉m-te zentrale Moment einer PDF (Aussagen relativ vom Mittelwert)

0.Moment: M₀ = 1
1.Moment: M₁ = Mittelwert

2.Zentrale Moment: M̃ₘ = Varianz σ²
3. 👉 "Schiefe" der PDF
4. 👉 "Wölbung" der PDF
Bsp:
#n-tes Moment eines Datensatzes
def moment(data, n):
return np.sum(data**n)/len(data)

Additional Stuff
np.argmax(), np.where()
Bayes Theorem (3blue1brown)
Bayesian Statistics
Probability Density Function, Probability Mass Function
Mode, Median, FWHM

Week 10 #

Binomial-/Poisson Verteilung, Zentraler Grenzwertsatz, Gauss Verteilung

Week 11 # (Likelihood Function ausgelassen)

Likelihood Funktion, Lineares Fitten von Polynomen

Annahme: Polynomieller Zusammenhang
👉 Messgrösse y(x) = f(x, a) = Σₙ ₌ ₀ᵐ(aₙxⁿ) , a = (a₀,..., aₘ)

Likelihood Funktion keine Wahrscheinlichkeitsverteilung

Log-Likelihood Funktion

Maximum Likelihood

Lineares Fitten nicht immer Sinnvoll wenn z.B. kein Physikalisches Modell zum Fitten benutzt wird
Minimieren der Summe der Residuenquadrate
S = Σₙ ₌ ₁ᴺ(wᵢ(yᵢ - f(xᵢ, a))²), wᵢ = 1/σᵢ²
Als Funktion:
def S_(x, y, sigma, f, a):
return np.sum((y - f(x,a))**2 / sigma**2)

Bsp:
# Wertebereiche für a0 und a1 definieren
a0_range = np.linspace(-0.5, 1.5, 50)
a1_range = np.linspace(0, 2, 60)

# Array für die berechneten S initialisieren
S = np.zeros(shape=(50, 60))

# S für alle Kombinationen berechnen
for i, a0 in enumerate(a0_range):
for j, a1 in enumerate(a1_range):
S[i, j] = np.sum((y_val - (a0 + a1 * x_val))**2 / sigma_y**2)

im = ax.pcolormesh(a0_range, a1_range, np.log(S).T, shading='nearest')
fig.colorbar(im, label=r'$\log S$')
ax.set_xlabel('$a_0$ (N)')
ax.set_ylabel('$a_1$ (N/cm)')
Bsp:

Analytische Methode
Nâ = Y Normalmatrix 👉 â = N⁻¹Y
â = (â₀,..., âₘ)ᵀ, N = ((Σᵢwᵢ, Σᵢwᵢxᵢ),(Σᵢwᵢxᵢ, Σᵢwᵢxᵢ²))ᵀ, Y = (Σᵢwᵢyᵢ, Σᵢwᵢxᵢyᵢ)ᵀ
wᵢ = 1/σᵢ²
Bsp 1:
Explizite Berechnung bei Grad 2:
w = 1/sigmaF**2

N = np.array([[np.sum(w), np.sum(w * x)], [np.sum(w * x), np.sum(w * (x**2))]])
Y = np.array([np.sum(w * F), np.sum(w * x * F)])
Ninv = np.linalg.inv(N) Matrix Invertieren

fitParams = Ninv @ Y , @ oder np.dot(Ninv, Y) Matrixmultiplikation (❗️auf Dimension achten❗️)
#a0, a1 = fitParams

sigma_a0 = np.sqrt(Ninv[0, 0])
sigma_a1 = np.sqrt(Ninv[1, 1])
Diagonaleinträge der Kovarianzmatrix sind die Standardabw. (sigma) der Fitparameter

Bsp 2:
Fit-Funktion für Polynome bel. Ordnung:
#pre: datasets x, y, sigma(y), Polynomgrad deg
#post: Kovarianzmatrix, Fitparameter (Spalten)vektor
def linearFit(x, y, sigma, deg):
w = 1/sigma**2
N = np.zeros(shape=(deg, deg))
Y = np.zeros(shape=(deg))

for i in range(deg):
Y[i] = np.sum(w)*(np.sum(x)**i)*np.sum(y)
for j in range(deg):
N[i, j] = np.sum(w)*np.sum(x)**(i+j)

#kovarianzmatrix
Ninv = np.linalg.inv(N)

fitParams = Ninv @ Y

return Ninv, fitParams

fit_n = np.zeros(len(x))
for index, x_i in enumerate(x):
sum_i = 0
for n, a_n in enumerate(fitParams_n):
sum_i += a_n * x_i**n

fit_n[index] = sum_i

import matplotlib.gridspec as gs

gs0 = gs.GridSpec(nrows=2, ncols=3, height_ratios=[3, 1], hspace=.1, figure=fig)
👉 ax = fig.add_subplot(gs0[0, 0])
ax.set_xticklabels([]) Entfernen der Achsenindizes
ax.text(x, y, "text") Text im Plot

Additional Stuff
Underfitting 👉 Abweichung von Datenpunkten und Fit, Struktur in den Residuen
Overfitting 👉 Residuen zufällig Verteilt (gut) aber Fitparameter verlieren physikalische Bedeutung also n-1 fittet den Datensatz vielleicht genauso gut

a.errorbar(x_val, y_val, sigma_y, capsize=3, linestyle='None', marker='.')
np.zeros(shape=(x, y))
Likelihood Function
Linear Regression (video)

Week 12 #

Fitten von nicht linearen Funktionen, Gradientenverfahren

Week 13 #

Machine Learning, Entscheidungsbäume, Lineare Regression, Logistische Regression, R2-Score

import pandas as pd

pandas basics
df = pd.read_csv('file.csv') "dataframe"
df.head() erste 5 Zeilen anzeigen
df[5:10] slicing wie bei numpy 👉 Spalten 5-9
df['Spaltenname1', 'Spaltenname2',...]
df.drop(['Spaltenname1', 'Spaltenname2', ...], axis=1) Spalte ausschliessen

Decision Trees

from sklearn

sklearn.model_selection import train_test_split

sklearn.tree import DecisionTreeClassifier

sklearn.tree import plot_tree

sklearn.metrics import accuracy_score

Test und Trainingssatz erstellen, Tree plotten, Accuracy Score bestimmen
Bsp:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, train_size=0.7)
train size sollte grösse als test sein, wenn nur test angegeben wird, dann ist train das Komplement davon
clf = DecisionTreeClassifier(max_depth=4).fit(X_train, y_train)
plot_tree(clf)
y_pred = clf.predict(X_test)
print('Accuracy Score: {}'.format(accuracy_score(y_pred, y_test)))

Neue Predictions mit trainiertem Modell 👉 clf.predict(df2)

Linear Regression

from sklearn

sklearn.linear_model import LinearRegression

sklearn.metrics import r2_score

R2-Score

Test und Trainingssatz erstellen, R2-Score bestimmen ähnlicher Ablauf wie bei Linear Regression
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
reg = LinearRegression().fit(X_train, y_train)
y_pred = reg.predict(X_test)
print("R2-Score: {:.3f}".format(r2_score(y_test, y_pred)))

Logistic Regression same wie oben...

from sklearn

sklearn.linear_model import LogisticRegression

logreg = LogisticRegression(max_iter=1000).logreg.fit(X_train, y_train) optional aber oft gut

Week 1 #

Basics, Arrays / Numpy-Arrays, Laden und Speichern von Daten

Week 2 #

Funktionen, Mittelwert / Standardabweichung, Histogramm, Normalverteilung

Week 3 #

Auflösung (des Signalwerts) einer Messung, Oszillierendes Signal & Samplingrate

Week 4 #

Fehler des Mittelwertes (mit Gauss), Gausssche Fehlerfortpflanzung

Week 5 #

Kovarianz, Autokovarianz f(t), Korrelationskoeffizient

Week 6 #

Fouriertransformation (Discrete Fourier Transform DFT), Spektrale Leistungsdichte (Power Spectral Density PSD)

Week 7 #

Rauschen (in PSD), Parseval-Theorem, Glätten, gleitender Mittelwert, Filtern

Week 8 "🏖️" #

Week 9 # (Bayesian Statistics ausgelassen)

Bayesian/Frequentist approach, Wahrscheinlichkeitsverteilung (Charakteristika, Momente), Probability Mass/Density Function (PMF/PDF)

Week 10 #

Binomial-/Poisson Verteilung, Zentraler Grenzwertsatz, Gauss Verteilung

Week 11 # (Likelihood Function ausgelassen)

Likelihood Funktion, Lineares Fitten von Polynomen

Week 12 #

Fitten von nicht linearen Funktionen, Gradientenverfahren

Week 13 #

Machine Learning, Entscheidungsbäume, Lineare Regression, Logistische Regression, R2-Score

Week 14 #

Grid Search, (K-Fold) Cross-Validation, Over-/Underfitting, Neural Network

Week 15 #

Filtern mit Faltungsmatrizen (, k-means Clustering in 2D)

Wall of Fame#