Neural Metamaterial Families
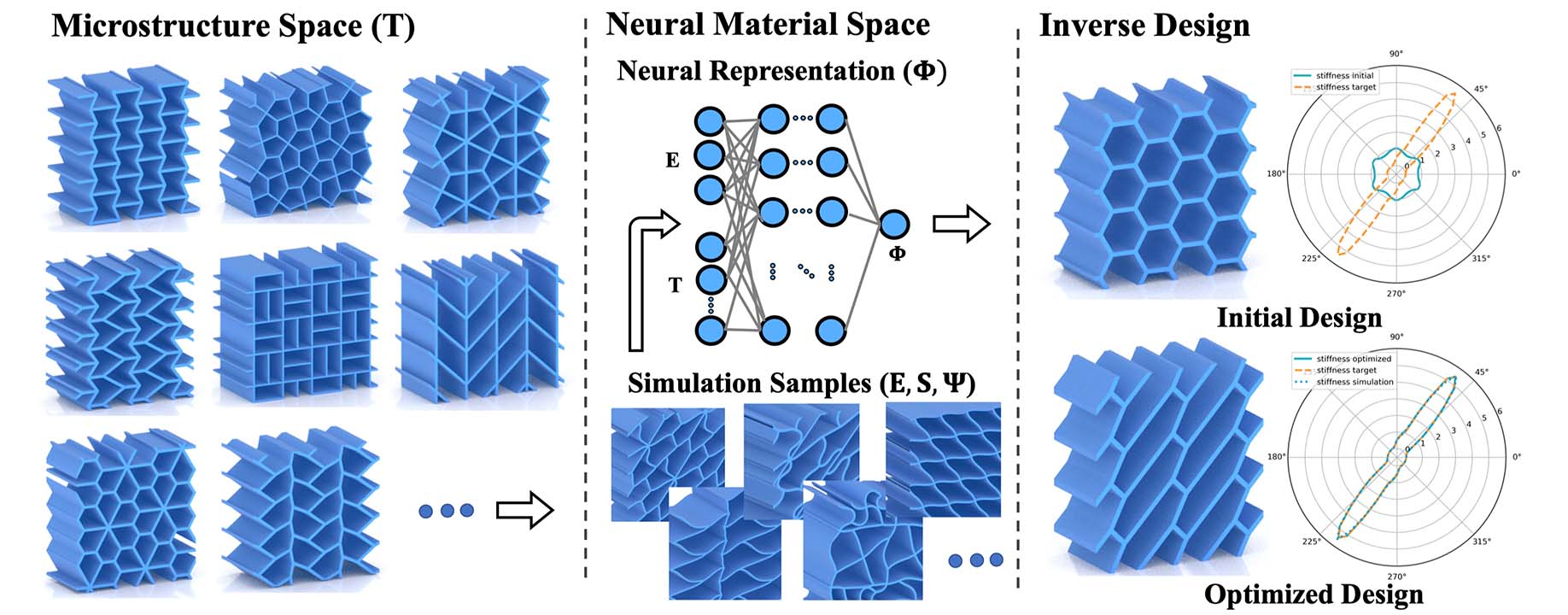
Nonlinear metamaterials with tailored mechanical properties have applications in engineering, medicine, robotics, and beyond. While modeling their macromechanical behavior is challenging in itself, finding structure parameters that lead to ideal approximation of high-level performance goals is a challenging task. In this work, we propose Neural Metamaterial Networks (NMN) -- smooth neural representations that encode the nonlinear mechanics of entire metamaterial families. Given structure parameters as input, NMN return continuously differentiable strain energy density functions, thus guaranteeing conservative forces by construction. Though trained on simulation data, NMN do not inherit the discontinuities resulting from topological changes in finite element meshes. They instead provide a smooth map from parameter to performance space that is fully differentiable and thus well-suited for gradient-based optimization. On this basis, we formulate inverse material design as a nonlinear programming problem that leverages neural networks for both objective functions and constraints. We use this approach to automatically design materials with desired strain-stress curves, prescribed directional stiffness and Poisson ratio profiles. We furthermore conduct ablation studies on network nonlinearities and show the advantages of our approach compared to native-scale optimization.
Neural Subspaces
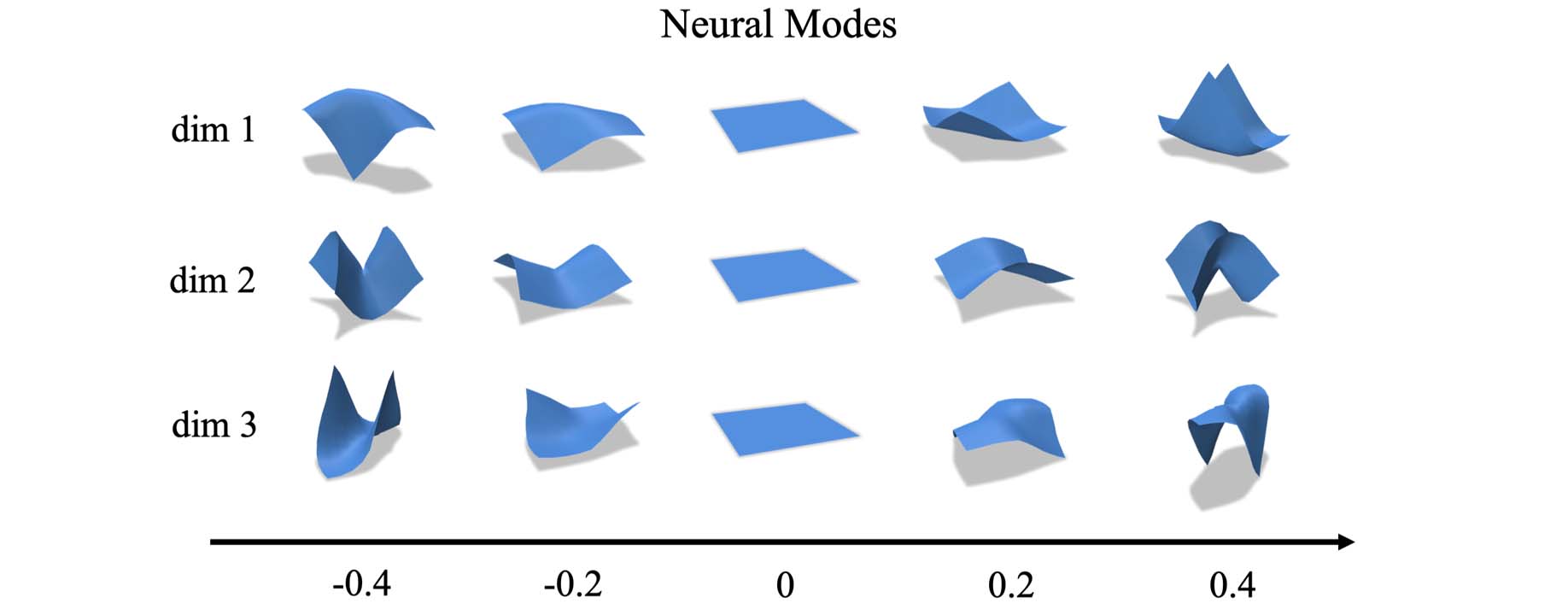
We propose a self-supervised approach for learning physics-based subspaces for real-time simulation. Existing learning-based methods construct subspaces by approximating pre-defined simulation data in a purely geometric way. However, this approach tends to produce highenergy configurations, leads to entangled latent space dimensions, and generalizes poorly beyond the training set. To overcome these limitations, we propose a self-supervised approach that directly minimizes the system’s mechanical energy during training. We show that our method leads to learned subspaces that reflect physical equilibrium constraints, resolve overfitting issues of previous methods, and offer interpretable latent space parameters.
Neural Cloth Simulation

We propose a method that leverages graph neural networks, multi-level message passing, and unsupervised training to enable real-time prediction of realistic clothing dynamics. Whereas existing methods based on linear blend skinning must be trained for specific garments, our method is agnostic to body shape and applies to tight-fitting garments as well as loose, free-flowing clothing. Our method furthermore handles changes in topology (e.g., garments with buttons or zippers) and material properties at inference time. As one key contribution, we propose a hierarchical message-passing scheme that efficiently propagates stiff stretching modes while preserving local detail. We empirically show that our method outperforms strong baselines quantitatively and that its results are perceived as more realistic than state-of-the-art methods.
Neural Topology Optimization
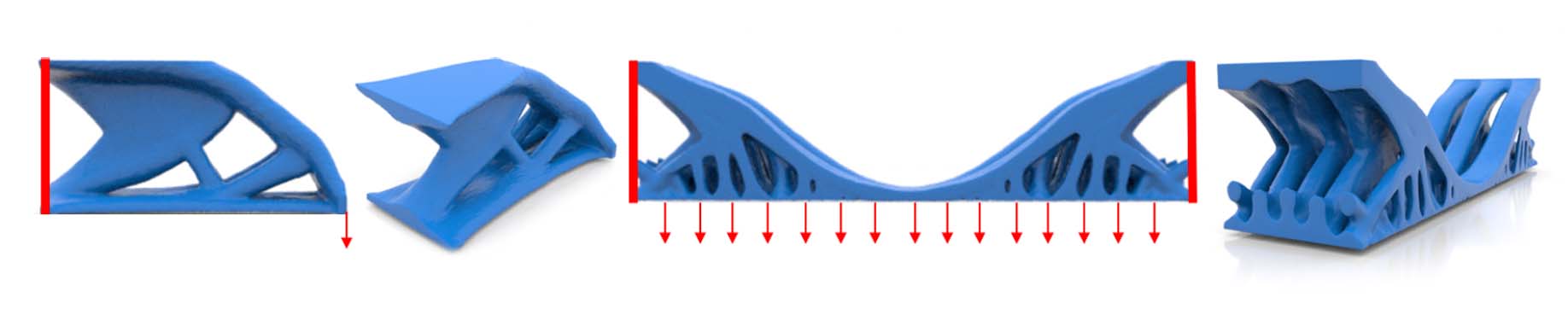
Recent advances in implicit neural representations show great promise when it comes to generating numerical solutions to partial differential equations. Compared to conventional alternatives, such representations employ parameterized neural networks to define, in a mesh-free manner, signals that are highly-detailed, continuous, and fully differentiable. In this work, we present a novel machine learning approach for topology optimization—an important class of inverse problems with high-dimensional parameter spaces and highly nonlinear objective landscapes. To effectively leverage neural representations in the context of mesh-free topology optimization, we use multilayer perceptrons to parameterize both density and displacement fields. Our experiments indicate that our method is highly competitive for minimizing structural compliance objectives, and it enables self-supervised learning of continuous solution spaces for topology optimization problems.