Structured Materials

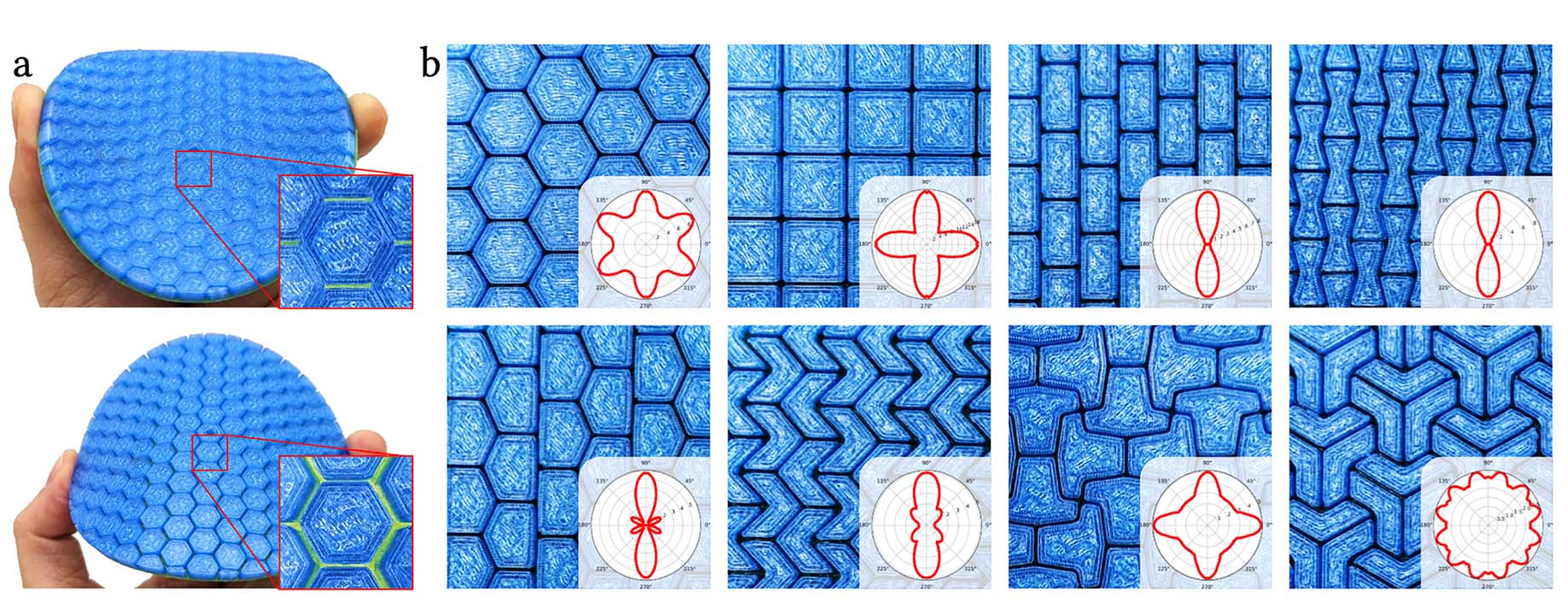
We present a computational approach for modeling the mechanical behavior of flexible scaled sheet materials—3D-printed hard scales embedded in a soft substrate. Balancing strength and flexibility, these structured materials find applications in protective gear, soft robotics, and 3D-printed fashion. To unlock their full potential, however, we must unravel the complex relation between scale pattern and mechanical properties. To address this problem, we propose a contact-aware homogenization approach that distills nativelevel simulation data into a novel macromechanical model. This macro-model combines piecewise-quadratic uniaxial fits with polar interpolation using circular harmonics, allowing for efficient simulation of large-scale patterns. We apply our approach to explore the space of isohedral scale patterns, revealing a diverse range of anisotropic and nonlinear material behaviors. Through an extensive set of experiments, we show that our models reproduce various scale-level effects while offering good qualitative agreement with physical prototypes on the macro-level.

We propose a comprehensive approach to characterizing the mechanical properties of structured sheet materials, i.e., planar rod networks whose mechanics and aesthetics are inextricably linked. We establish a connection between the complex mesoscopic deformation behavior of such structures and their macroscopic elastic properties through numerical homogenization. Our approach leverages 3D Kirchhoff rod simulation in order to capture nonlinear effects for both in-plane and bending deformations. We apply our method to different families of structures based on isohedral tilings — a simple yet extensive and aesthetically interesting group of space-filling patterns. We show that these tilings admit a wide range of material properties, and our homogenization approach allows us to create concise and intuitive descriptions of a material’s direction-dependent macromechanical behavior that are easy to communicate even to non-experts. We perform this characterization for an extensive set of structures and organize these data in a material browser to enable efficient forward exploration of the aesthetic-mechanical space of structured sheet materials. We also propose an inverse design method to automatically find structure parameters that best approximate a user-specified target behavior.

Stripe patterns are ubiquitous in nature and everyday life. While the synthesis of these patterns has been thoroughly studied in the literature, their potential to control the mechanics of structured materials remains largely unexplored. In this work, we introduce Differentiable Stripe Patterns—a computational approach for automated design of physical surfaces structured with stripe-shaped bi-material distributions. Our method builds on the work by Knöppel and colleagues [2015] for generating globally-continuous and equally-spaced stripe patterns. To unlock the full potential of this design space, we propose a gradient-based optimization tool to automatically compute stripe patterns that best approximate macromechanical performance goals. Specifically, we propose a computational model that combines solid shell finite elements with XFEM for accurate and fully-differentiable modeling of elastic bi-material surfaces. To resolve non-uniqueness problems in the original method, we furthermore propose a robust formulation that yields unique and differentiable stripe patterns. We combine these components with equilibrium state derivatives into an end-to-end differentiable pipeline that enables inverse design of mechanical stripe patterns. We demonstrate our method on a diverse set of examples that illustrate the potential of stripe patterns as a design space for structured materials. Our simulation results are experimentally validated on physical prototypes.

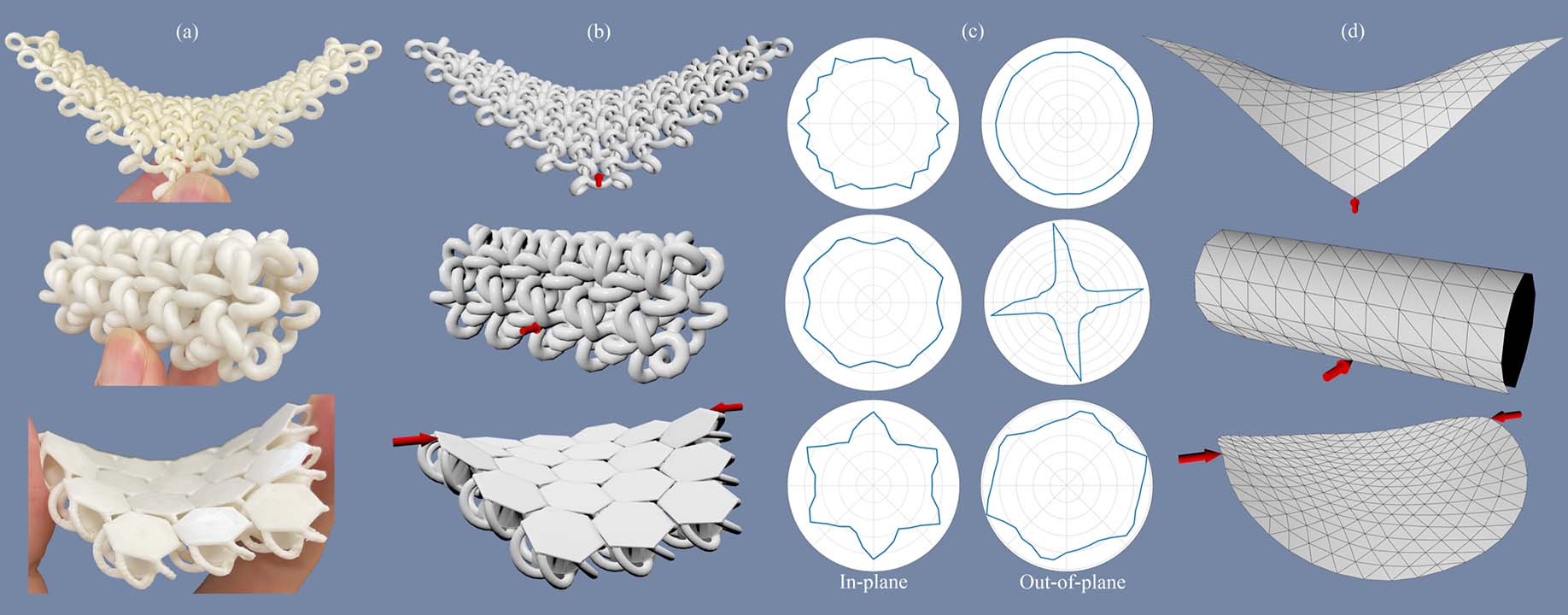
We present a method for computational modeling, mechanical characterization, and macro-scale simulation of discrete interlocking materials (DIM)3D-printed chainmail fabrics made of quasi-rigid interlocking elements. Unlike conventional elastic materials for which deformation and restoring force are directly coupled, the mechanics of DIM are governed by contacts between individual elements that give rise to anisotropic deformation constraints. To model the mechanical behavior of these materials, we propose a computational approach that builds on three key components. (a): we explore the space of feasible deformations using native-scale simulations at the per-element level. (b): based on this simulation data, we introduce the concept of strain-space boundaries to represent deformation limits for inand out-of-plane deformations, and (c): we use the strain-space boundaries to drive an efficient macro-scale simulation model based on homogenized deformation constraints. We evaluate our method on a set of representative discrete interlocking materials and validate our findings against measurements on physical prototypes.

We present a method for designing and fabricating MetaSilicones—composite silicone rubbers that exhibit desired macroscopic mechanical properties. The underlying principle of our approach is to inject spherical inclusions of a liquid dopant material into a silicone matrix material. By varying the number, size, and locations of these inclusions as well as their material, a broad range of mechanical properties can be achieved. The technical core of our approach is formed by an optimization algorithm that, combining a simulation model based on extended finite elements (XFEM) and sensitivity analysis, computes inclusion distributions that lead to desired stiffness properties on the macroscopic level. We explore the design space of MetaSilicone on an extensive set of simulation experiments involving materials with optimized uni- and bi-directional stiffness, spatially-graded properties, as well as multi-material composites. We present validation through standard measurements on physical prototypes, which we fabricate on a modified filament-based 3D printer, thus combining the advantages of digital fabrication with the mechanical performance of silicone elastomers.