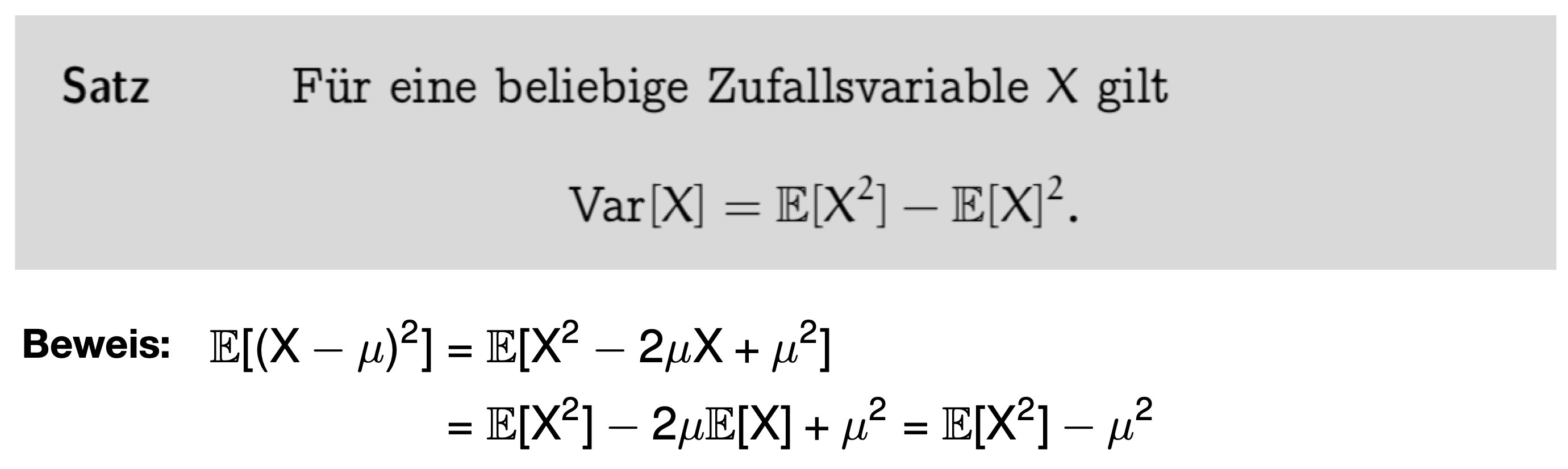AnW Übung 7 Read-Up

Kontakt

E-Mail: toffermann@ethz.ch

Website/ Unterlagen: https://n.ethz.ch/~toffermann/

Plan für heute

• Stoff diese Woche

• In-Class Exercise

Vorlesung 11 & 12

• Varianz Recap

  

  

• Rechenregeln, Erwartungswert und Varianz
  • $\mathbb E[X+Y] = \mathbb E[X] + \mathbb E[Y]$
  • $\mathbb E[X\cdot Y] = \mathbb E[X] \cdot \mathbb E[Y]; X,Y$ unabhängig
  • $\text{Var}[X+Y] = \text{Var}[X] + \text{Var}[Y]; X,Y$ unabhängig
  • $\text{Var}[aX+b] = a^2\text{Var}[X]$

• Markov

  Gilt für Zufallsvariable $X$, dass $W_X \subseteq \R^+_0$ ist, dann gilt:

  $P[X \geq t] \leq \frac{\mathbb E[X]}{t}, t > 0$

  • Beispiel Aufgabe

    

    • Lösung:

      $2/3$

• Chebyshev

  $P[|X-\mathbb E [X]| \geq t] \leq \frac{\text{Var}[X]}{t^2}, t > 0$

  

  • Lösung:

    $4/n$

• Chernoff

  Ist $X$ die Summe von $n$ Bernoulli verteilten Zufallsvariablen ($X = \sum_i X_i, X_i \sim \text{Ber}(p_i)$), so gilt:

  $P[X \geq (1+\delta)\mathbb E[X]] \leq e^{-\frac 1 3 \delta^2 \mathbb E[X]}$

  

  • Lösung

    $e^{-n/24}$

• Dynamic Programming Exercise

• Randomisierte Algorithmen

  

• Las-Vegas

  Ein Las-Vegas Algorithmus ist ein Algorithmus der immer eine richtige Antwort gibt. Die Laufzeit ist hierbei aber eine Zufallsvariable.

  Beispiel: Quick-Sort, oder:

  

  Zum Auffinden eines Indexes an dem $1$ steht (wir nehmen an in $A$ ist immer mind. eine $1$). Dann gibt der Algorithmus irgendwann (wenn er richtig rät) eine richtige Antwort. Die Laufzeit des Algorithmus ist aber durch eine Zufallsvariable gegeben, da wir keine Garantie geben können, nach wie vielen Schritten der Algorithmus das erste Mal “Glück” hat.

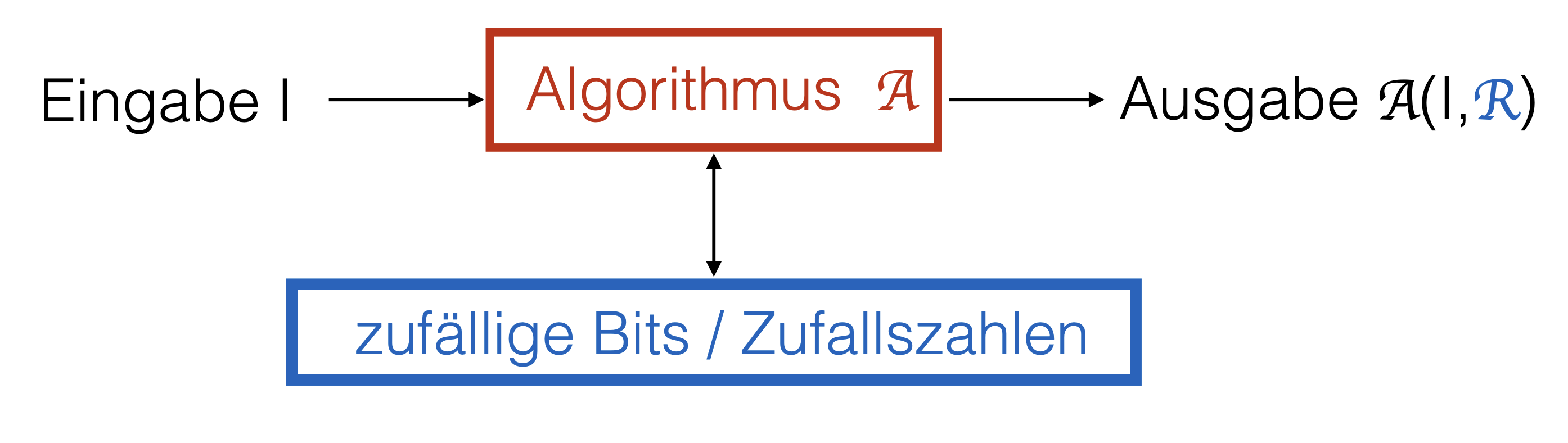
  Ein Las-Vegas Algorithmus ist auch immer ein (besonderer) Monte-Carlo Algorithmus:

  

  Dementsprechend ist ein Las-Vegas Algorithmus “stärker” als ein Monte-Carlo Algorithmus. Man kann wie in der obigen Abbildung zu sehen jeden Las-Vegas Algorithmus in einen Monte-Carlo Algorithmus umwandeln.

• Monte-Carlo Algorithmus

  Ein Monte-Carlo Algorithmus hat immer polynomielle Laufzeit, gibt aber zuweilen falsche Ausgaben aus.

  Beispiel:

  

  Wit verwenden Monte-Carlo Algorithmen oft für Entscheidungsprobleme, für eine gegebene Eingabe soll “JA” oder “NEIN” ausgegeben werden.

  Es gibt Monte-Carlo Algorithmen mit einseitigem und zweiseitigem Fehler:

  

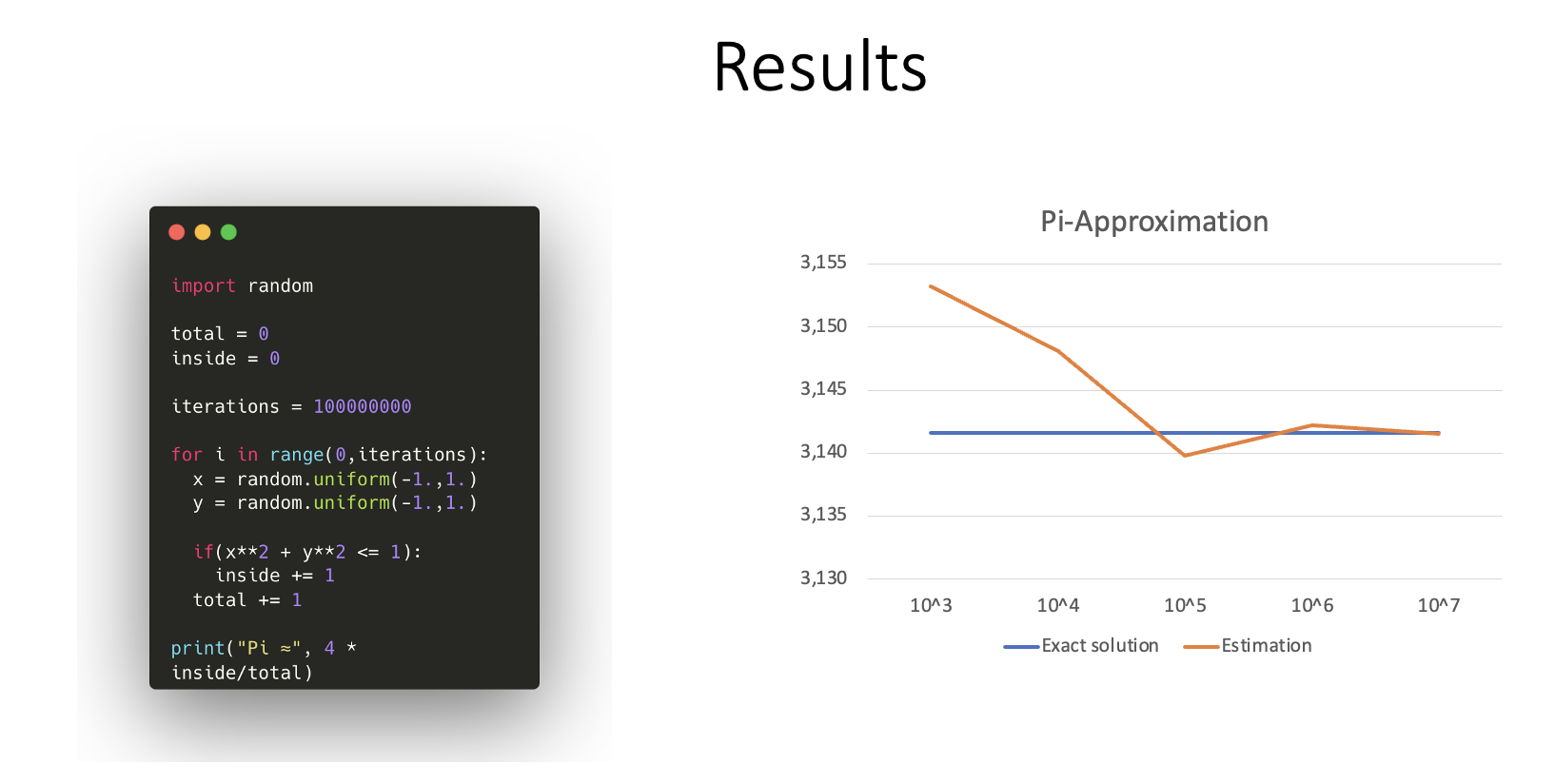
• Target-Shooting

  Gegeben: $U, S \subseteq U$, bestimme $\frac{|S|}{|U|}$:

  Wir brauchen eine Funktion (am besten effizient berechenbar) $f: U \mapsto \{0,1\}$, die für jedes Element entscheidet, ob $u \in U$ auch in $S$ liegt ($f(u) = 1$) oder nicht ($f(u) = 0$).

  Wir wählen nun $N$ mal zufällige Elemente $u_i$ aus $U$, und geben $\frac{\sum_{i=1}^N f(u_i)} N$ zurück. Intuitiv ist dieser Wert auch genau eine Annäherung an $\frac{|S|}{|U|}$.

  

• Pi-Approx Beispiel