AnW Übung 12 Read-Up

Kontakt

E-Mail: toffermann@ethz.ch

Website/ Unterlagen: https://n.ethz.ch/~toffermann/

Plan für heute

• Minitest

• Theorie Recap

• In-Class Exercise

Themen der Vorlesung

• MIN-CUT Problem

  Multi-Graph $G = (V,E)$ gegeben (ungerichtet, ungewichtet, ohne Schleifen)

  Wir fragen uns wie viele Kanten $C \subseteq E$ müssen entfernt werden, so dass $G'=(V,E\backslash C)$ nicht mehr zusammenhängend ist.

  Mit $\mu (G)$ bezeichnen wir die kleinste Anzahl an zu entfernenden Kanten:

  $\mu(G) = \min_{C \subseteq E, (V,E\backslash C) \text{ unzusammenhängend}}|C|$

  

  

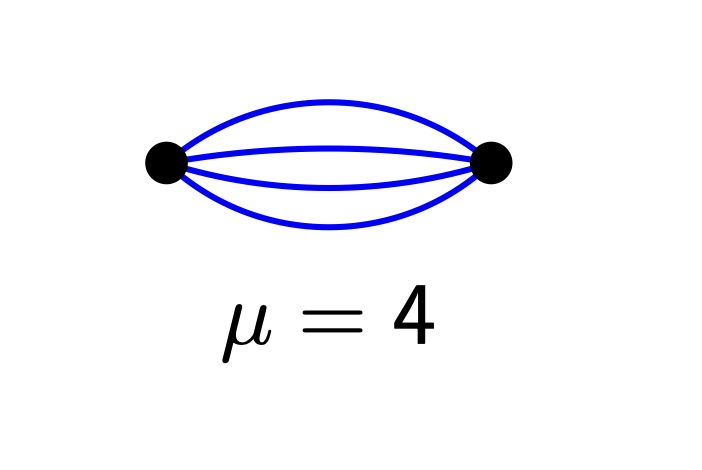
  $\deg(v) \coloneqq$ Anzahl anliegende Kanten

  Es gilt:

  • Handschlag-Lemma: $2|E| = \sum_{v \in V} deg(v)$
  • $\mu(G) \leq \min_{v \in V} deg(v)$

• Deterministisch mit Flüssen

  Wir wissen, wie man den kleinsten $s$-$t$-Schnitt berechnet (maximaler Fluss von $s$ nach $t$). Dieser gibt an wie viele Kanten, bzw. wie viel Kantengewicht man minimal entfernen muss, um $s$ von $t$ zu trennen.

  Für unseren Multigraphen können wir unser Netzwerk folgendermaßen bilden:
  Nehmen wir Multigraph:
  

  

  Wir können diese $4$ ungewichteten Kanten in unserem Netzwerk als eine Kante mit Gewicht $4$ darstellen. Weil die Kante ungerichtet ist müssen wir in dem Netzwerk zwei Kanten mit Gewicht $4$ für beide Richtungen einfügen.

  Ist die Kante mit Gewicht $4$ dann Teil des minimalen Schnittes, so müssen in unserem ursprünglichen Multigraphen ebenso alle $4$ Kanten entfernt werden um den Zusammenhang zu zerstören.

  ---

  Betrachten wir eine optimale MIN-CUT Lösung $C$ mit $|C| = \mu(G)$. Nehmen wir an $G' = (V, E\backslash C)$ besteht dann aus zwei Zusammenhangskomponenten $A,B$.

  Wenn wir nur einen $s$-$t$-Schnitt für unsere Lösung betrachten könnte es sein, dass sowohl $s$, als auch $t$ in der selben Zusammenhangskomponente liegen. Wenn wir dann den minimalen $s$-$t$-Schnitt berechnen kann es sein, dass wir nicht mehr die beste Lösung $|C|$ finden.

  Dementsprechend müssen wir für ein fixes $s$ einmal alle Knoten $v \in V \backslash \{s\}$ als unser $t$ durchprobieren.

  Laufzeit ein Durchlauf: $O(mn\log n)$ (Dynamic Trees)

  Wir probieren alle $n-1$ Knoten $v \in V \backslash \{s\}$ als unser $t$ aus. Ergibt Laufzeit $O(mn^2\log n) = O(n^4\log n)$, wegen $m \leq \binom n 2 = O(n^2)$

• Erster randomisierte Ansatz

  Der Algorithmus basiert auf Kantenkontraktion.

  Kontrahieren wir eine Kante $e = (u,v)$ so werden $u,v$ zu einem neuen Knoten $z$, der weiterhin mit allen Nachbarn von $u$, sowie $v$ verbunden ist. Es gehen alle Kanten zwischen $u,v$ verloren:

  

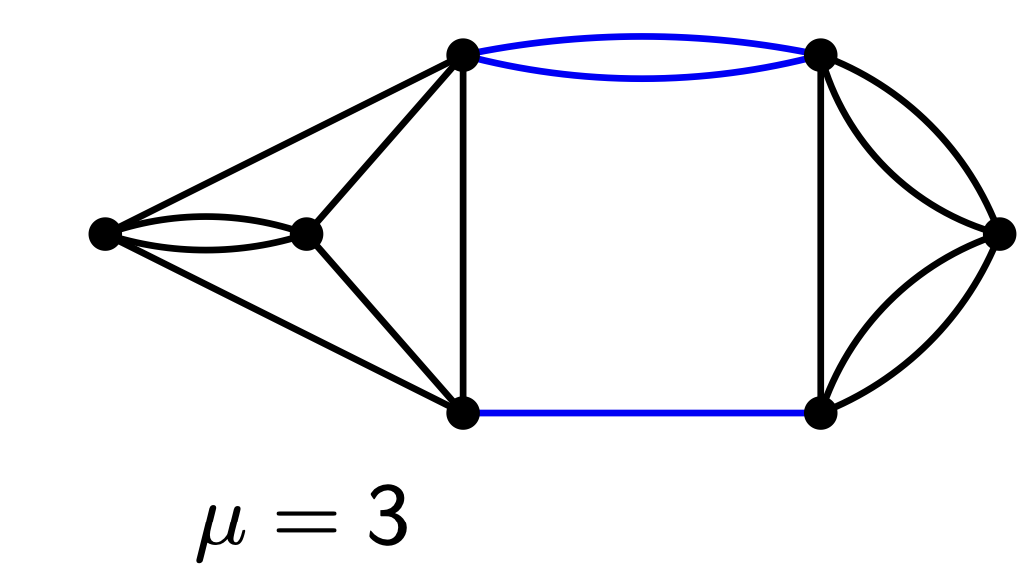
  Im folgenden Graphen sind die blauen Kanten $C$:

  

  Kontrahieren wir Kanten die nicht blau sind $G \rightarrow G'$, so gilt $\mu(G) = \mu(G')$. Haben wir also “Glück” und ziehen immer Kanten die nicht blau sind, und kontrahieren diese, so finden wir am Ende zwei Knoten zwischen denen die blauen Kanten liegen. Die Anzahl dieser Kanten gibt $|C|$ an.

  Wenn wir aus versehen eine blaue Kante ziehen und kontrahieren, dann kann es sein, dass der minimale Schnitt in $G'$ größer ist als der in $G$.

  Wir fassen zusammen:

  • $e \in E: \mu(G') \geq \mu(G)$
  • $e \not \in C : \mu(G') = \mu(G)$

  (Beachte, dass das Beispiel mit den blauen Kanten nicht komplett richtig ist. Es gibt möglicher Weise mehrere minimale Schnitte $C_1,C_2,...$ und nicht nur einen. Die Aussagen sind immer so gemeint, dass wenn wir $e$ ziehen, es weiterhin einen minimalen Schnitt in $G$ ohne $e$ gibt. Diese Kanten wären dann die “nicht blauen” Kanten)

  Wir leiten daraus folgenden Algorithmus ab:

  

  Wie oben beschrieben kann CUT($G$) mit einer Wahrscheinlichkeit $p$ die richtige Antwort liefern (Wenn wir immer nicht-blaue Kanten wählen). Was ist aber $p$?

  Wir nehmen an, dass $k \coloneqq \mu(G) = |C|$ für einen gegebenen minimalen Schnitt $C$ und betrachten $p_n = P[\mu(G) = \mu(G\backslash e)]$:

  • $P[\mu(G) = \mu(G\backslash e)] \geq P[e \not \in C]$, weil $e$ somit definitiv “nicht-blau” ist (gibt es noch einen anderen minimalen Schnitt $C_1$ so könnte es sein, dass wir $e \in C$ wählen dürfen und $C_1$ damit beibehalten, daher ist oben ein “$\geq$” und kein “$=$”)
  • $P[e \not \in C] = 1 - \frac{|C|}{|E|} \geq 1 -\frac{k}{kn/2} = 1-2/n$,
    
    $|C| = k$ und $|C| = k \implies \deg(v) \geq k \implies |E| = \frac 1 2 \sum_v \deg(v) \geq \frac{kn} 2$
  • Also insgesamt: $p_n = P[\mu(G) = \mu(G\backslash e)] \geq 1-2/n = \frac{n-2}{n}$

  $p_n$ gibt an wie wahrscheinlich es ist, dass wir im ersten Schritt von CUT($G$) keinen Fehler machen ($n$ gibt nur die Anzahl der Knoten vor der Kontraktion an).

  Damit können wir eine untere Schranke für $p$ geben:
  
  $p \geq p_n \cdot p_{n-1} \cdot ... \cdot p_3 = \frac{n-2}{n}\cdot \frac{n-3}{n-1} \cdot \frac{n-4}{n-2} \cdot ... \cdot \frac{2}{4} \cdot \frac{1}{3} = \frac{2}{n(n-1)} = 1/ \binom n 2$

  Wir wiederholen den Algorithmus $\lambda \binom n 2$ mal. Die Wahrscheinlichkeit, dass immer eine falsche Antwort gegeben wird ist $\leq (1- \frac{1}{\binom n 2})^{\lambda \binom n 2} \leq e^{-\lambda \frac{1}{\binom n 2}\binom n 2} = e^{- \lambda}$. Angewandte Ungleichung: $(1-x)^n \leq e^{-nx}$

  Also gibt es eine richtige Antwort mit Wahrscheinlichkeit $\geq 1-e^{-\lambda}$. Für $\lambda = \log n$ haben wir Laufzeit $O(n^4\log n)$ und Fehler $1/n$.

  • Laufzeit ein Durchlauf CUT($G$) ist $O(n^2)$
  • $O(\binom n 2 \log n) = O(n^2 \log n)$ viele Durchläufe
  • Also insgesamt $O(n^4\log n)$

• Bei $t$ Knoten Abbrechen

  Wir beobachten, dass der Algorithmus in den letzten Schritten die meisten Fehler macht:

  $p \geq p_n \cdot p_{n-1} \cdot ... \cdot p_3 = \frac{n-2}{n}\cdot \frac{n-3}{n-1} \cdot \frac{n-4}{n-2} \cdot ... \cdot \underbrace{ \frac{2}{4}}_{0.5} \cdot \underbrace{ \frac{1}{3}}_{0.33} = \frac{2}{n(n-1)} = 1/ \binom n 2$

  Daher stoppen wir den Algorithmus wenn wir noch $t$ Knoten übrig haben (welches $t$ das Beste ist bestimmen wir gleich) und rechnen danach mit einem bekannten Algorithmus weiter.

  Den Algorithmus den wir in den letzen $t$ Runden verwenden ist der randomisierte Algorithmus von oben mit $\lambda = 1$

  • Laufzeit $O(n^4)$
  • Richtig mit Wahrscheinlichkeit $p_t \geq 1 - e^{-1}$

  $p \geq \frac{n-2}{n}\cdot \frac{n-3}{n-1} \cdot \frac{n-4}{n-2} \cdot ... \cdot \frac{t}{t+2} \cdot \frac{t-1}{t+1} \cdot p_t \geq \frac{t(t-1)}{n(n-1)} \cdot (\frac{e-1}{e})$

  Wenn wir diesen Algorithmus nun $\lambda/p$ mal laufen lassen erhalten wir wieder ein richtiges Ergebnis mit Wahrscheinlichkeit $\geq 1-e^{-\lambda}$.

  Laufzeit:

  • Ein Durchlauf kontrahiert $n-t$ Knoten in Zeit $O(n(n-t))$ und rechnet danach in Zeit $O(t^4)$ den Rest zu Ende insgesamt abgeschätzt $O(n^2+t^4)$
  • Wir haben $\lambda/p = \lambda(\frac{en(n-1)}{(e-1)t(t-1)}) = O(\lambda\frac{n^2}{t^2})$ Wiederholungen
  • Multiplikation ergibt finale Laufzeit: $O(\lambda(\frac{n^4}{t^2}+n^2t^2))$
  • Für $t = \sqrt n$ hat man Laufzeit: $O(\lambda n^3)$

• Bootstrapping

  Im obigen Schritt haben wir den Algorithmus “abgebrochen”, wenn es noch $t$ Knoten gab und ab da mit einem bekannten Algorithmus weiter gerechnet.

  Dafür haben wir unseren ersten randomisierten CUT($G$)-Algo mit $\lambda =1$ verwendet. Dieser hatte Laufzeit $O(n^4)$.

  Gerade haben wir aber einen Algorithmus kreiert der für $\lambda =1$ mit der selben Erfolgswahrscheinlichkeit (selben lower-bound) in $O(n^3)$ statt $O(n^4)$ läuft. Deswegen können wir das gleiche Verfahren nochmals mit dem $O(n^3)$ statt $O(n^4)$ Algorithmus starten und bekommen für ein neues $t$ dann einen noch schnelleren Algorithmus den wir wieder anstelle des $O(n^3)$ Algorithmus einsetzen können.

  Im Grenzwert erhält man dann einen $O(n^2\text{poly}(\log n))$ Algorithmus.

In-Class Exercise