Inflatable Structures from Inextensible Material

M. Skouras, B. Thomaszewski, P. Kaufmann, A. Garg, B. Bickel, E. Grinspun, M. Gross
ACM Transactions on Graphics (Proc. ACM SIGGRAPH 2014)
PDF Video Supplemental
We propose an interactive, optimization-in-the-loop tool for designing inflatable structures. Given a target shape, the user draws a network of seams defining desired segment boundaries in 3D. Our method computes optimally-shaped flat panels for the segments, such that the inflated structure is as close as possible to the target while satisfying the desired seam positions. Our approach is underpinned by physics-based pattern optimization, accurate coarse-scale simulation using tension field theory, and a specialized constraint-optimization method. Our system is fast enough to warrant interactive exploration of different seam layouts, including internal connections, and their effects on the inflated shape. We demonstrate the resulting design process on a varied set of simulation examples, some of which we have fabricated, demonstrating excellent agreement with the design intent.
Shape Optimization for Inflatable Rubber Membranes
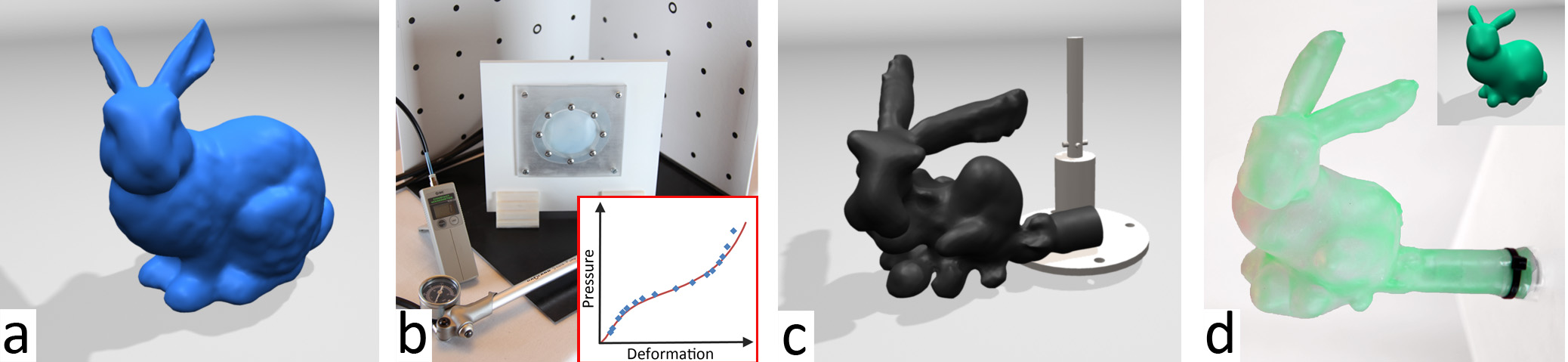
M. Skouras, B. Thomaszewski, B. Bickel, M. Gross
Computer Graphics Forum (Eurographics 2012), 31(2), 2012
Project Page
This paper presents an automatic process for fabrication-oriented design of custom-shaped rubber balloons. We cast computational balloon design as an inverse problem: given a target shape, we compute an optimal balloon that, when inflated, approximates the target as closely as possible. To solve this problem numerically, we propose a novel physics-driven shape optimization method, which combines physical simulation of inflatable elastic membranes with a dedicated constrained optimization algorithm. We validate our approach by fabricating balloons designed with our method and comparing their inflated shapes to the results predicted by simulation. An extensive set of manufactured sample balloons demonstrates the shape diversity that can be achieved by our method.
Surfaces Assembled from Discrete Elements
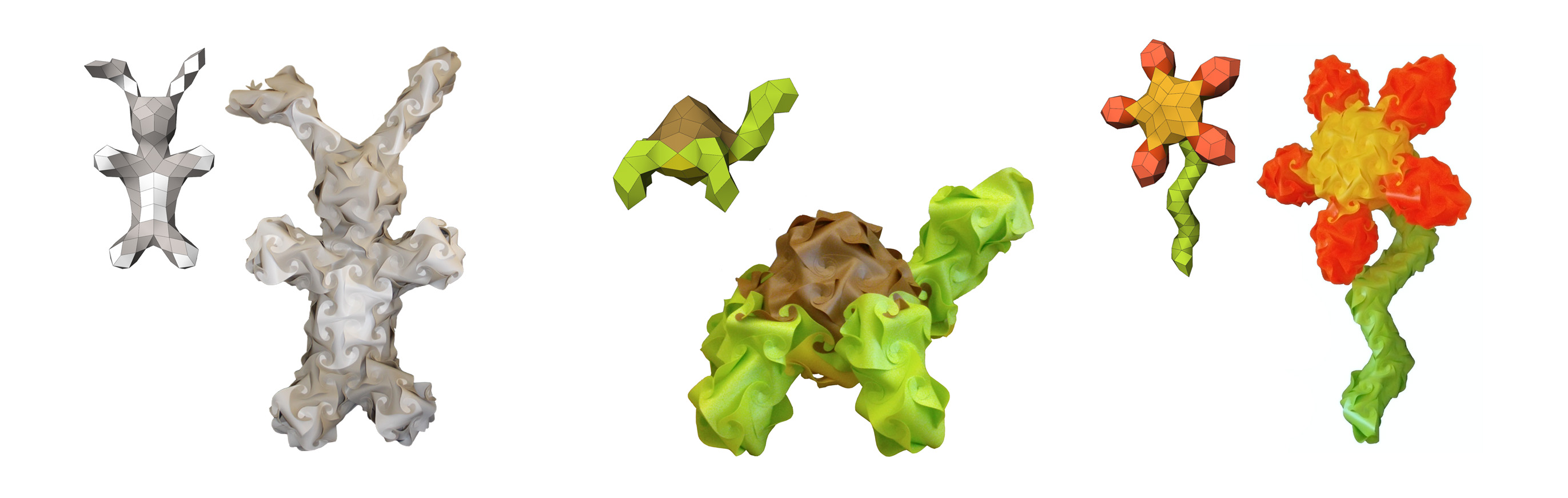
We present an interactive tool for designing physical surfaces made from flexible interlocking quadrilateral elements of a single size and shape. With the element shape fixed, the design task becomes one of finding a discrete structure—i.e., element connectivity and binary orientations—that leads to a desired geometry. In order to address this challenging problem of combinatorial geometry, we propose a forward modeling tool that allows the user to interactively explore the space of feasible designs. Paralleling principles from conventional modeling software, our approach leverages a library of base shapes that can be instantiated, combined, and extended using two fundamental operations: merging and extrusion. In order to assist the user in building the designs, we furthermore propose a method to automatically generate assembly instructions. We demonstrate the versatility of our method by creating a diverse set of digital and physical examples that can serve as personalized lamps or decorative items.
Ornamental Curve Networks
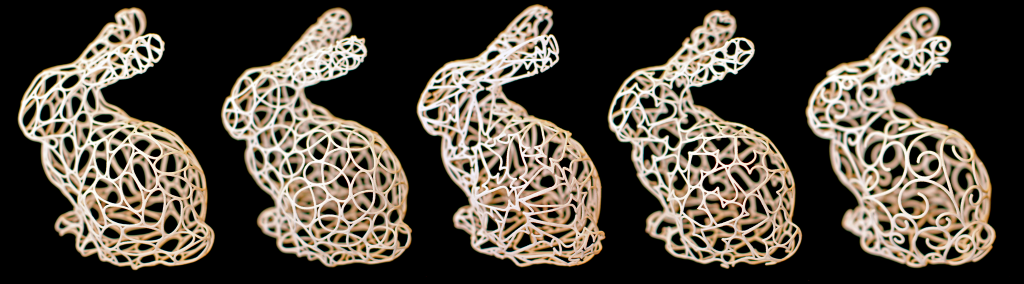
We present a computational tool for designing ornamental curve networks—structurally-sound physical surfaces with user-controlled aesthetics. In contrast to approaches that leverage texture synthesis for creating decorative surface patterns, our method relies on user-defined spline curves as central design primitives. More specifically, we build on the physically-inspired metaphor of an embedded elastic curve that can move on a smooth surface, deform, and connect with other curves. We formalize this idea as a globally coupled energy-minimization problem, discretized with piece-wise linear curves that are optimized in the parametric space of a smooth surface. Building on this technical core, we propose a set of interactive design and editing tools that we demonstrate on manually-created layouts and semi-automated deformable packings. In order to prevent excessive compliance, we furthermore propose a structural analysis tool that uses eigenanalysis to identify potentially large deformations between geodesically-close curves and guide the user in strengthening the corresponding regions. We used our approach to create a variety of designs in simulation, validated with a set of 3D-printed physical prototypes.
Elastic Rod Networks

We present a computational tool for fabrication-oriented design of flexible rod meshes. Given a deformable surface and a set of deformed poses as input, our method automatically computes a printable rod mesh that, once manufactured, closely matches the input poses under the same boundary conditions. The core of our method is formed by an optimization scheme that adjusts the cross-sectional profiles of the rods and their rest centerline in order to best approximate the target deformations. This approach allows us to locally control the bending and stretching resistance of the surface with a single material, yielding high design flexibility and low fabrication cost.