Elo rating for football
During my PhD our department was asked by Austrian national television to predict the outcome of the remaining rounds of the Austrian national football league. I wrote a simple ELO based prediction algorithm in Python. Not to be taken seriously or used for for betting purposes, it’s a simplistic toy model. The bookmakers are much better at this.
import numpy as npimport copyimport scipy as spimport csvimport matplotlib.pyplot as pltimport seaborn as snsimport operatorsns.set()# Import past resultspast_results = []with open('AUT.csv') as csvfile: readCSV = csv.reader(csvfile, delimiter=',') numGames = 0 for row in readCSV: if row[2]=="2018/2019": past_results.append({"ht": row[5], "at": row[6], "hg": int(row[7]), "ag": int(row[8]), "round": numGames//6}) numGames += 1numRounds=numGames//6
# Future matchesremaining_matches = [('LASK Linz','Wacker Innsbruck'), ('Salzburg',"Sturm Graz"), ('Austria Vienna',"Altach"), ('Mattersburg','Rapid Vienna'), ("Admira",'St. Polten'), ('Hartberg','AC Wolfsberger'), ("Sturm Graz","Austria Vienna"), ("Rapid Vienna","Hartberg"), ("St. Polten","Mattersburg"), ("Wacker Innsbruck","Salzburg"), ("Altach","LASK Linz"), ("AC Wolfsberger","Admira")]
# Extract a list of teamsteams = []for result in past_results: if result['ht'] not in teams: teams.append(result['ht'])
# Compute current standingspoints = {}goals_scored = {}goals_conceded = {}goals = {}for team in teams: points[team] = 0 goals[team] = 0 goals_scored[team] = 0 goals_conceded[team] = 0for result in past_results: goals_scored[result["ht"]] += result["hg"] goals_conceded[result["ht"]] += result["ag"] goals_scored[result["at"]] += result["ag"] goals_conceded[result["at"]] += result["hg"] goals[result["at"]] += result["ag"] - result["hg"] points[result["ht"]] += 3 if result["hg"]>result["ag"] else 0 if result["hg"]<result["ag"] else 1 points[result["at"]] += 0 if result["hg"]>result["ag"] else 3 if result["hg"]<result["ag"] else 1for team in teams: goals[team] = goals_scored[team] - goals_conceded[team]class eloPredictor(): def __init__(self, homefield_adv=100, weight=lambda nRound:20, expected_result=lambda DeltaH: 1/(10**(-DeltaH/400)+1), probs_from_E=lambda E: [1-E-np.exp(-(E-.5)**2/2/.28**2)/3/2,np.exp(-(E-.5)**2/2/.28**2)/3,E-np.exp(-(E-.5)**2/2/.28**2)/3/2]): self.score_rate = {} self.concede_rate = {} self.probs_from_E = probs_from_E self.weight = weight self.elo = {} self.homefield_adv = homefield_adv self.__expected_result__ = expected_result
# Compute elo from past results for team in teams: self.elo[team] = [1500] self.score_rate[team] = goals_scored[team]/numRounds self.concede_rate[team] = goals_conceded[team]/numRounds for result in past_results: G = (abs(result["hg"]-result["ag"])+11)/8 W = 1 if result["hg"]>result["ag"] else 0 if result["hg"]<result["ag"] else .5 Wh = self.expected_result(result["ht"],result["at"]) Wa = 1 - Wh self.elo[result["ht"]].append(self.elo[result["ht"]][-1]+self.weight(result["round"])*G*(W-Wh)) self.elo[result["at"]].append(self.elo[result["at"]][-1]+self.weight(result["round"])*G*(1-W-Wa))
# compute adjusted elo diff with homefield advantage def elo_diff(self,teamH,teamA): return self.elo[teamH][-1] - self.elo[teamA][-1] + self.homefield_adv
# compute expected result using supplied formula def expected_result(self,teamA,teamB): return self.__expected_result__(self.elo_diff(teamA,teamB))
# compute winning probabilities from expected result and supplied formula def probabilities(self,teamA,teamB): E = self.expected_result(teamA,teamB) return self.probs_from_E(E) pD = self.pDraw(E) pW = E - pD/2 pL = 1 - pD - pW return[pL,pD,pW]
# plot elo development def plot_elo_history(self): plt.figure(num=None, figsize=(10, 8), facecolor='w', edgecolor='k') for team, elos in self.elo.items(): plt.plot(elos,label=team) plt.legend() plt.show()
# compute probability of advancing to the next round from sampling def advProb(self,nSample=1000): self.points_after = copy.copy(points) self.match_results = {} for match in remaining_matches: self.match_results[match] = np.random.choice([0,1,3], nSample, p=self.probabilities(match[0],match[1])) match_resultsA = copy.copy(self.match_results[match]) match_resultsA[match_resultsA == 3] = -1 match_resultsA[match_resultsA == 0] = 3 match_resultsA[match_resultsA == -1] = 0 self.points_after[match[0]] += self.match_results[match] self.points_after[match[1]] += match_resultsA
# Count number of samples where each team is in the top six # Rule for equal points: sort teams by goals from past games self.numTopSix = {team: 0 for team in teams} for k in range(nSample): points_temp = {team: [self.points_after[team][k],goals[team]] for team in teams} for team in sorted(points_temp, key=points_temp.get, reverse=True)[:6]: self.numTopSix[team] += 1 orderedTeams = sorted(self.numTopSix, key=lambda x: self.numTopSix[x],reverse=True) return {team: self.numTopSix[team]/nSample for team in orderedTeams}
def advProbPois(self,nSample=1000): self.points_after = copy.copy(points) self.goals = copy.copy(goals) self.match_results = {} for match in remaining_matches: goalsA = np.random.poisson(lam=(self.score_rate[match[0]]+self.concede_rate[match[1]])/2,size=nSample) goalsB = np.random.poisson(lam=(self.score_rate[match[1]]+self.concede_rate[match[0]])/2,size=nSample) self.goals[match[0]] += goalsA self.goals[match[1]] += goalsB self.points_after[match[0]] += np.array([3 if gA>gB else 0 if gA<gB else 1 for (gA,gB) in zip(goalsA.tolist(),goalsB.tolist())]) self.points_after[match[1]] += np.array([0 if gA>gB else 3 if gA<gB else 1 for (gA,gB) in zip(goalsA.tolist(),goalsB.tolist())]) self.numTopSix = {team: 0 for team in teams} for k in range(nSample): points_temp = {team: [self.points_after[team][k],self.goals[team][k]] for team in teams} for team in sorted(points_temp, key=points_temp.get, reverse=True)[:6]: self.numTopSix[team] += 1 orderedTeams = sorted(self.numTopSix, key=lambda x: self.numTopSix[x],reverse=True) return {team: self.numTopSix[team]/nSample for team in orderedTeams}
# plot advancing probabilities def plot_adv_prob(self,nSample=1000,method="elo"): if method=="elo": probs=self.advProb(nSample=nSample) else: probs=self.advProbPois(nSample=nSample) plt.figure(num=None, figsize=(10, 8), facecolor='w', edgecolor='k') plt.xticks(rotation='vertical') plt.bar(probs.keys(),probs.values()) for i in range(12): plt.text(x = i-.72 , y = list(probs.values())[i]+.01, s = "{:10.3f}".format(list(probs.values())[i]), size = 12,color="red") plt.show()ELO history
With default parameters
eloPredictor().plot_elo_history()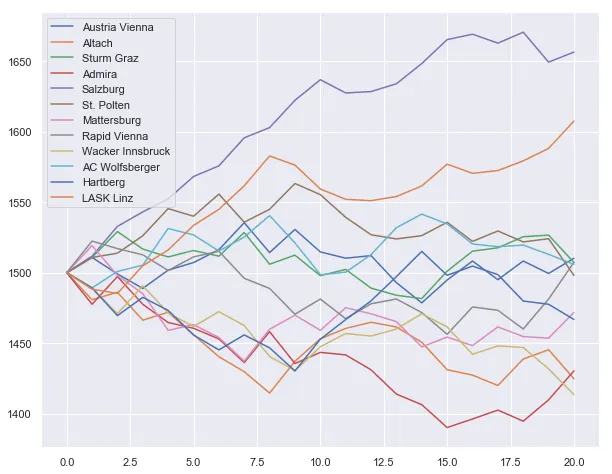
Without homefield advantage
eloPredictor(homefield_adv=0).plot_elo_history()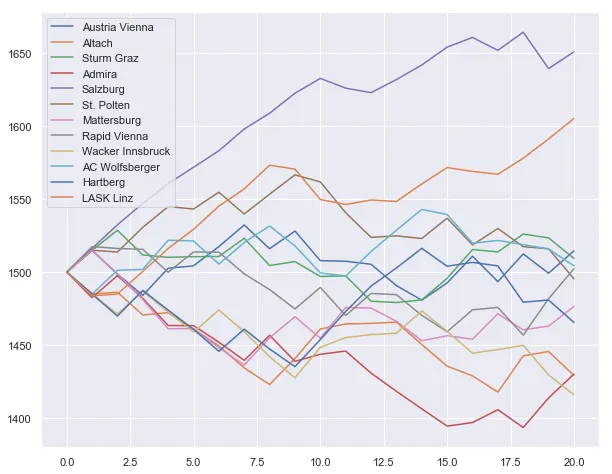
Double weight for the last five rounds
eloPredictor(weight=lambda round: 60 if round > 15 else 20).plot_elo_history()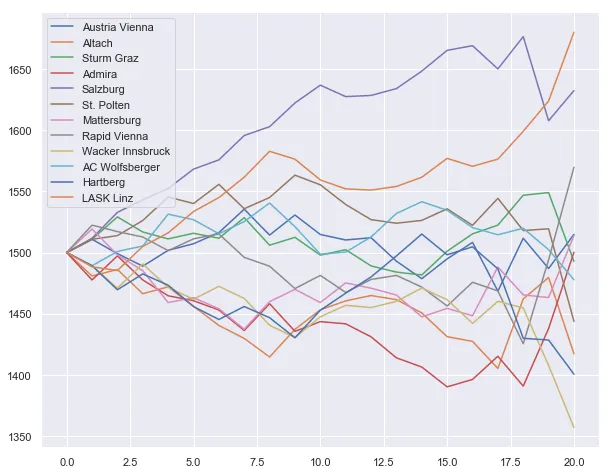
Prediction from ELO rating
Default parameters
eloPredictor().plot_adv_prob(nSample=50000)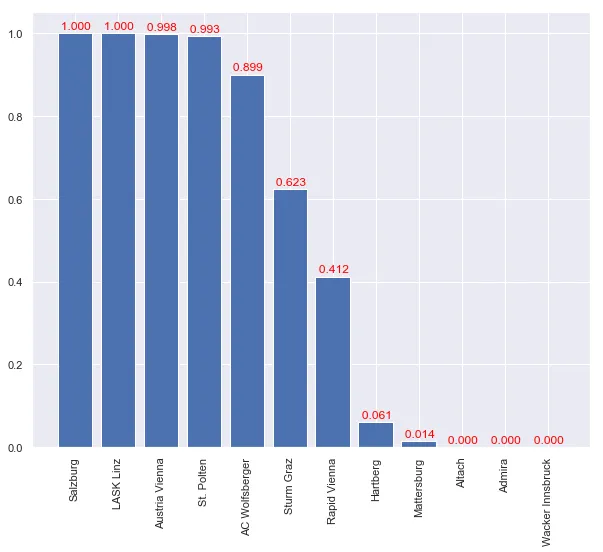
Assuming that in the remaining matches draw/win/loss are equally likely
eloPredictor(probs_from_E=lambda E: [1-E,0,E]).plot_adv_prob(nSample=10000)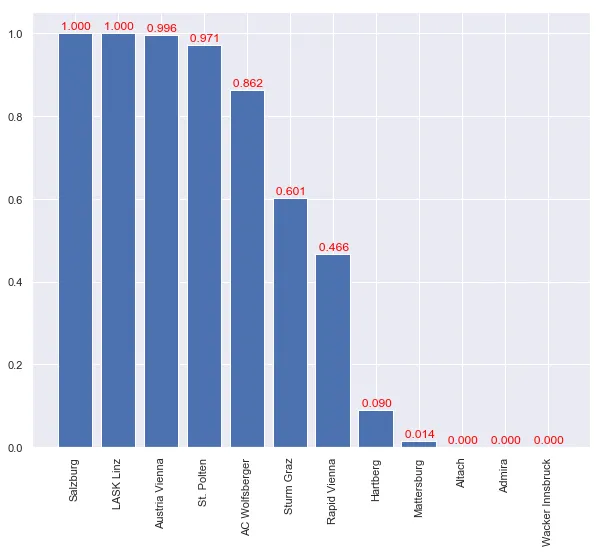
Assuming that the last five rounds carry a bigger weight. This changes the ELO development (see above)
eloPredictor(weight=lambda round: 60 if round > 14 else 20).plot_adv_prob(nSample=50000)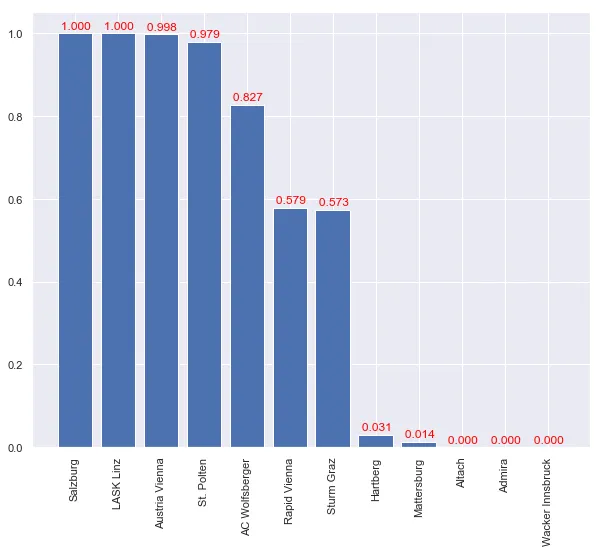
Poisson sampling
eloPredictor().plot_adv_prob(nSample=100000,method="Pois")
