Research Overview
Publications
-
1. Phase Transition in the Density of States of Quantum Spin Glasses
László Erdős, Dominik Schröder
Math. Phys. Anal. Geom.Vol. 17 (2014) | Issue 3-4
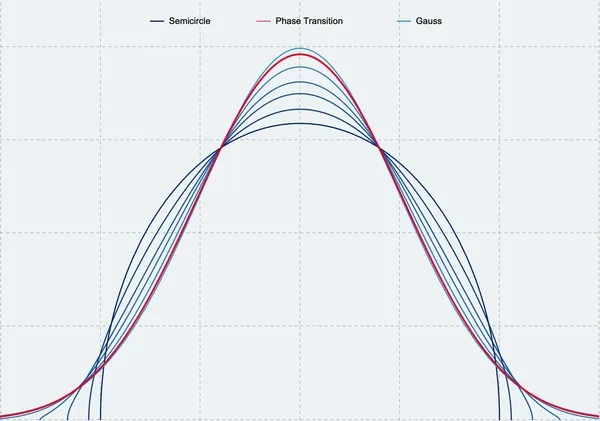
We demonstrate a transition between Gaussian and semicircular laws using q-Hermite polynomials. This work has inspired large amounts of follow-up research on the SYK model for quantum gravity.
-
2. Fluctuations of rectangular Young diagrams of interlacing Wigner eigenvalues
László Erdős, Dominik Schröder
Int. Math. Res. Not. IMRN(2018)
We study the rectangular Young diagrams obtained from interlacing eigenvalues and show that the limiting shape is given by the well known Vershik-Kerov-Logan-Shepp curve.
-
3. Fluctuations of functions of Wigner matrices
László Erdős, Dominik Schröder
Electron. Commun. Probab.Vol. 21 (2016)
We prove a CLT for the entrywise fluctuations of functions of random matrices. The use of Pleijel's formula makes our result applicable to all functions of bounded variation.
-
4. Random matrices with slow correlation decay
László Erdős, Dominik Schröder
Forum Math. SigmaVol. 7 (2017)
We prove universality for a large class of random matrices with correlated entries. This very general result has been used numerous times, also in more applied research.
-
5. Correlated random matrices: Band rigidity and edge universality
Johannes Alt, László Erdős, Torben Krüger, Dominik Schröder
Ann. Probab.Vol. 48 (2020)
We prove that also the edge statistics of general correlated Hermitian random matrices are universal. Our result implies that the eigenvalues in each support interval of the asymptotic density is deterministic with high probability.
-
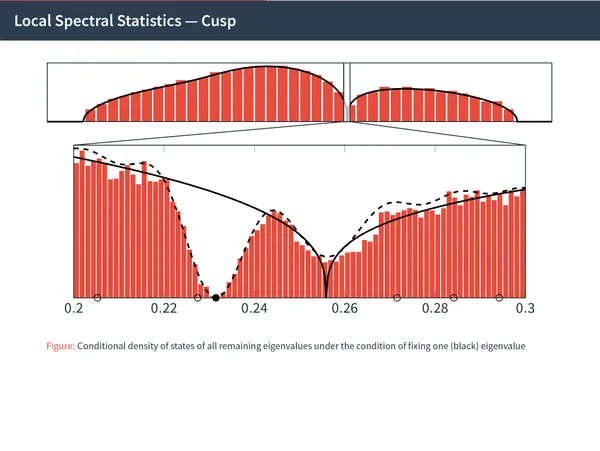
6. Cusp universality for random matrices I: local law and the complex Hermitian case
László Erdős, Torben Krüger, Dominik Schröder
Comm. Math. Phys.Vol. 378 (2020)
Hermitian random matrices can only feature three universal eigenvalue statistics: Sine in the bulk, Airy at square-root edges and Pearcey at cubic-root cusps. In this work we complete the universality program for those matrices by proving Pearcey-kernel universality at all cusp points.
-
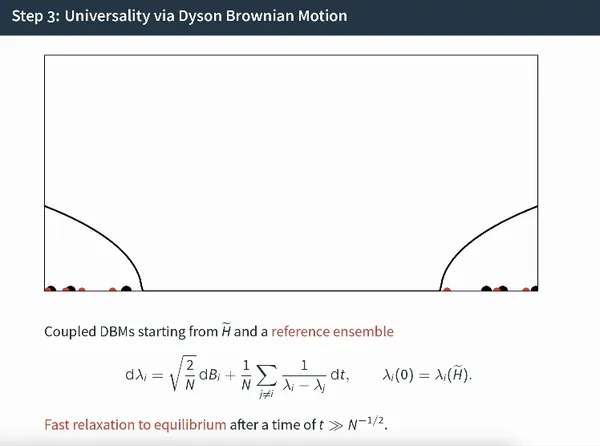
7. Cusp universality for random matrices, II: The real symmetric case
Giorgio Cipolloni, László Erdős, Torben Krüger, Dominik Schröder
Pure Appl. Anal.Vol. 1 (2019)
This is the companion result to the previous paper on cusp universality for complex Hermitian matrices. Lacking Brézin-Hikami-type integral formulae we resort to the more robust Dyson Brownian Motion approach.
-
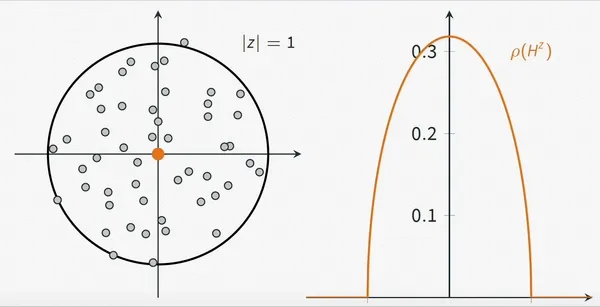
8. Edge universality for non-Hermitian random matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Probab. Theory Related FieldsVol. 179 (2021)
We prove that on the unit circle (the asymptotic boundary of the spectrum) the local eigenvalue statistics on non-Hermitian random matrices with IID entries are universal. This generalizes previous results on random matrices matching four Gaussian moments.
-
9. Optimal lower bound on the least singular value of the shifted Ginibre ensemble
Giorgio Cipolloni, László Erdős, Dominik Schröder
Probab. Math. Phys.Vol. 1 (2020)
Using the superbosonization technique we derive optimal lower bounds on the least singular value of shifted Ginibre random matrices.
-
10. Central limit theorem for linear eigenvalue statistics of non-Hermitian random matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Comm. Pure Appl. Math.Vol. 76 (2023)
We show that the linear statistics of random matrices with IID entries asymptotically are a rank-one perturbation of the Gaussian free field on the unit disc.
-
11. Fluctuation around the circular law for random matrices with real entries
Giorgio Cipolloni, László Erdős, Dominik Schröder
Electron. J. Probab.Vol. 26 (2021)
This is the companion paper to the corresponding result for complex random matrices. The limiting distribution in this case is a symmetrized version of the Gaussian Free Field.
-
12. Eigenstate thermalization hypothesis for Wigner matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Comm. Math. Phys.Vol. 388 (2021)
We prove that any deterministic matrix is approximately the identity in the eigenbasis of a large random Wigner matrix with very high probability and with an optimal error inversely proportional to the square root of the dimension, rigorously verifying the Eigenstate Thermalization Hypothesis.
-
13. Functional central limit theorems for Wigner matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Ann. Appl. Probab.Vol. 33 (2023)
We extend the classical CLTs for linear statistics functionally, in the sense that we prove the CLT for traces auf functions of Wigner matrices multiplied with arbitrary deterministic observables.
-
14. Thermalisation for Wigner matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
J. Funct. Anal.Vol. 282 (2022)
We extend key results from free probability on polynomials to arbitrary Sobolev functions. Applied to time Heisenberg evolution operators this proves the thermalization effect of the unitary group generated by Wigner matrices.
-
15. Normal fluctuation in quantum ergodicity for Wigner matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Ann. Probab.Vol. 50 (2022)
We prove a CLT for quadratic forms of eigenvectors of Wigner matrices with arbitrary deterministic matrices, considerably strengthening previous results on quantum unique ergodicity.
-
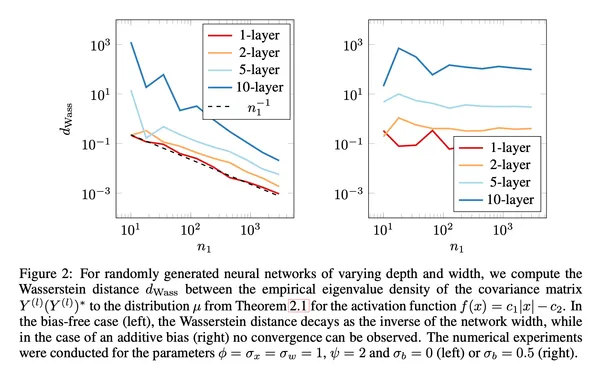
16. Analysis of one-hidden-layer neural networks via the resolvent method
Vanessa Piccolo, Dominik Schröder
NeurIPSVol. 34 (2021)
We provide an alternative derivation for the asymptotic spectrum of non-linear random matrices, based on the more robust resolvent model. Our approach in particular extends previous results on random feature models to the practically important case with additive bias.
-
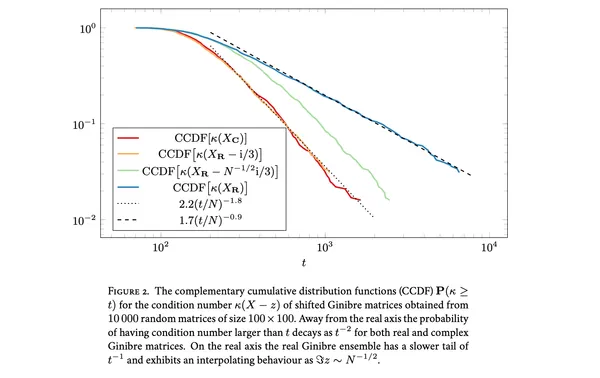
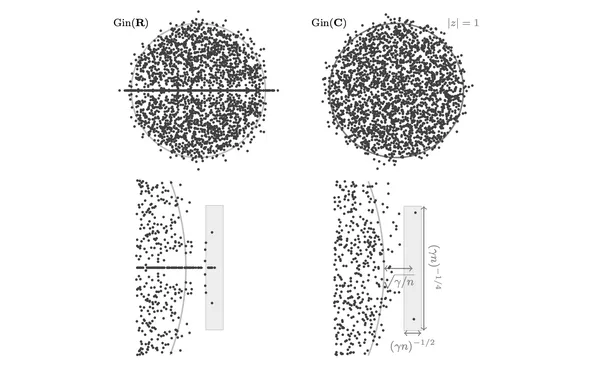
17. On the condition number of the shifted real Ginibre ensemble
Giorgio Cipolloni, László Erdős, Dominik Schröder
SIAM J. Matrix Anal. Appl.Vol. 43 (2022)
We show that complex shifts of real matrices have a stronger regularizing effect than real shifts. As a consequence we obtain improved bounds on the practically relevant condition number and demonstrate that our results give sharp asymptotics for the running time of the CG algorithm.
-
18. Density of Small Singular Values of the Shifted Real Ginibre Ensemble
Giorgio Cipolloni, László Erdős, Dominik Schröder
Ann. Henri PoincaréVol. 23 (2022)
We derive a precise asymptotic formula for the density of the small singular values of the real Ginibre matrix ensemble shifted by a complex parameter. In particular we prove that away from the real axis real and complex Ginibre matrices have the same local statistics.
-
19. Quenched universality for deformed Wigner matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Probab. Theory Related FieldsVol. 185 (2023)
Following Eugene Wigner's original vision, we prove that sampling the eigenvalue gaps within the bulk spectrum of a fixed (deformed) Wigner matrix yields the celebrated Wigner-Dyson-Mehta universal statistics with high probability.
-
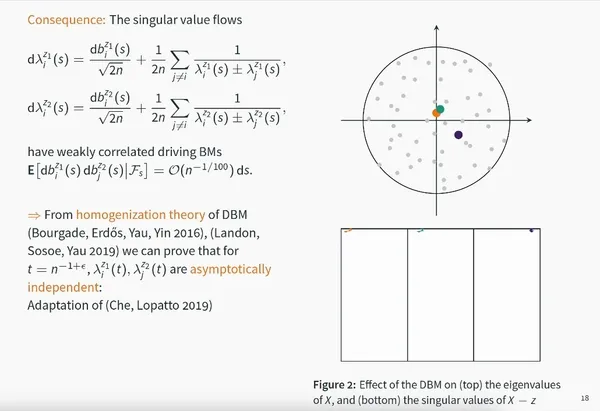
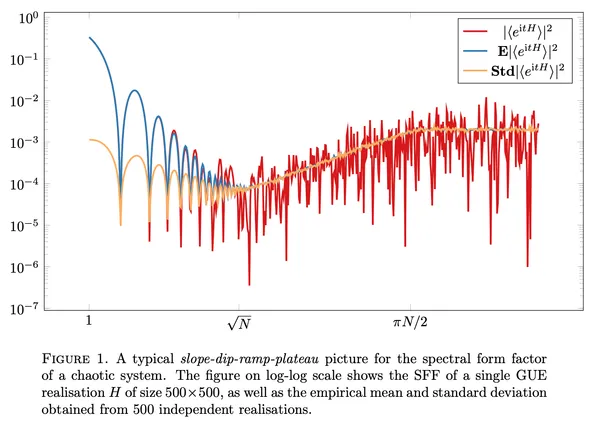
20. On the spectral form factor for random matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Comm. Math. Phys.Vol. 401 (2023)
In the physics literature the spectral form factor (SFF), the squared Fourier transform of the empirical eigenvalue density, is the most common tool to test universality for disordered quantum systems, yet previous mathematical results have been restricted only to two exactly solvable models. We rigorously prove the physics prediction on SFF up to an intermediate time scale for a large class of random matrices.
-
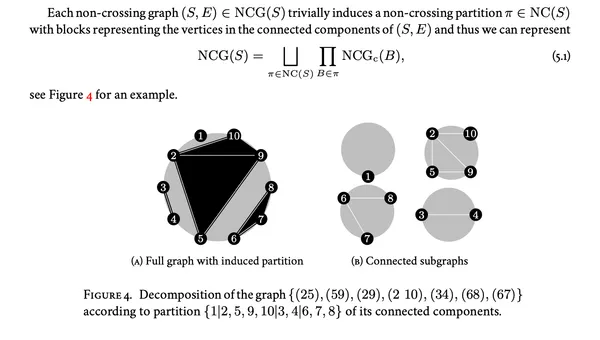
21. Optimal multi-resolvent local laws for Wigner matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Electron. J. Probab.Vol. 27 (2022)
We prove local laws for arbitrary products of resolvents of a Wigner random matrix with deterministic matrices in between. Our key finding is that the size of such products heavily depends on whether some of the deterministic matrices are traceless.
-
22. Rank-uniform local law for Wigner matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Forum Math. SigmaVol. 10 (2022)
We prove a general local law for Wigner matrices which optimally handles observables of arbitrary rank and thus it unifies the well-known averaged and isotropic local laws.
-
23. Directional extremal statistics for Ginibre eigenvalues
Giorgio Cipolloni, László Erdős, Dominik Schröder, Yuanyuan Xu
J. Math. Phys.Vol. 63 (2022)
We obtain Gumbel fluctuations for the maximal real part of eigenvalues of Ginibre matrices. Moreover, we show that the corresponding extreme eigenvalues asymptotically form a Poisson point process.
-
24. On the rightmost eigenvalue of non-Hermitian random matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder, Yuanyuan Xu
Preprint(2022)
We obtain a precise three-term expansion for the right-most eigenvalue of IID random matrices, precisely matching the corresponding result for Ginibre matrices which may be obtained with more algebraic methods.
-
25. Mesoscopic central limit theorem for non-Hermitian random matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Probab. Theory Relat. Fields(2023)
We extend our previous result on the CLT for the linear statistics of IID random matrices to the entire mesoscopic regime.
-
26. Optimal Lower Bound on Eigenvector Overlaps for non-Hermitian Random Matrices
Giorgio Cipolloni, László Erdős, Joscha Henheik, Dominik Schröder
Preprint(2023)
We show that already a small noise completely thermalizes the bulk singular vectors of arbitrary deterministic matrices. In particular we prove a strong form of Quantum Unique Ergodicity (QUE) with an optimal speed of convergence for such matrices.
-
27. Deterministic equivalent and error universality of deep random features learning
Dominik Schröder, Hugo Cui, Daniil Dmitriev, Bruno Loureiro
ICML(2023)
We show that the generalization error of deep random feature models is the same as the generalization error of Gaussian features with matched covariance, and derive an explicit expression for the generalization error.
-
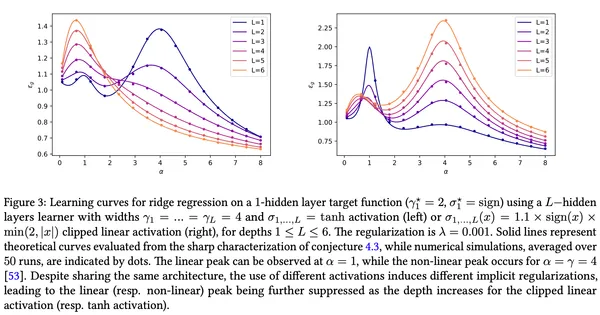
28. Asymptotics of Learning with Deep Structured (Random) Features
Dominik Schröder, Hugo Cui, Daniil Dmitriev, Bruno Loureiro
ICML 2024(2024)
We derive an approximative formula for the generalization error of deep neural networks with structured (random) features, confirming a widely believed conjecture. We also show that our results can capture feature maps learned by deep, finite-width neural networks trained under gradient descent.
-
29. Matrix Concentration Inequalities and Free Probability II. Two-sided Bounds and Applications
Afonso Bandeira, Giorgio Cipolloni, Ramon van Handel, Dominik Schröder
preprint(2024)
We determine the approximate location of the extreme eigenvalues for a large class of random matrix models. These two-sided bounds are fundamentally beyond the reach of classical matrix concentration inequalities.
Theses
-
In my BSc thesis I worked on topics related to random Schrödinger operators and the Feynman-Kac formula.
-
In my essay for the Part III course in Cambridge I studied breakthrough papers on interlacing polynomials by Marcus, Spielman and Srivastava. Using this innovative approach they proved the long standing Kadison-Singer conjecture from operator algebra theory, and proved the existence of bipartite Ramanujan graphs of arbitrary degree.
-
In my master thesis I worked on quantum spin glasses. The main novel finding was a phase transition between a semicircular and Gaussian density of states.
-
In my PhD thesis I worked on three challenging problems in random matrix theory: (1) Universality of random matrices with correlated entries, (2) Pearcey-kernel universality at cusp points, and (3) entrywise linear statistics and Young tableaux.
Research Rotations
- Limits to gene regulation due to crosstalk. with Gašper Tkačik Internal report (2015)
- Analyzing response of retinal neurons in fish and Generalization bounds for active task selection. with Christoph Lampert Internal report (2016)