Central limit theorem for linear eigenvalue statistics of non-Hermitian random matrices

Summary

We show that the linear statistics of random matrices with IID entries asymptotically are a rank-one perturbation of the Gaussian free field on the unit disc.

Main result

We study the fluctuations around the well known circular law, which asserts that the eigenvalues $\sigma_1,\ldots,\sigma_n$ of a random matrix with suitably scaled IID entries asymptotically are uniformly distributed on the unit disc in the sense

$$\frac{1}{n}\sum_i f(\sigma_i) \approx \frac{1}{\pi}\int_D f(z)\, \mathrm d^2 z.$$

Here we prove the corresponding CLT

$$\sum_i f(\sigma_i) \approx \mathcal N\Bigl(0,\frac{1}{4\pi}\lVert f\rVert_{L^2(D)}^2 + \frac{1}{2}\lVert f\rVert_{\dot H^{1/2}(\partial D)} + \kappa_4 \lvert \langle f\rangle_D - \langle f\rangle_{\partial D}\rvert^2 \Bigr)$$

extending previous result for analytic test functions $f$ or Gaussian matrices. The first two terms in the variance may be interpreted as the Gaussian Free Field on the unit disc.

Proof

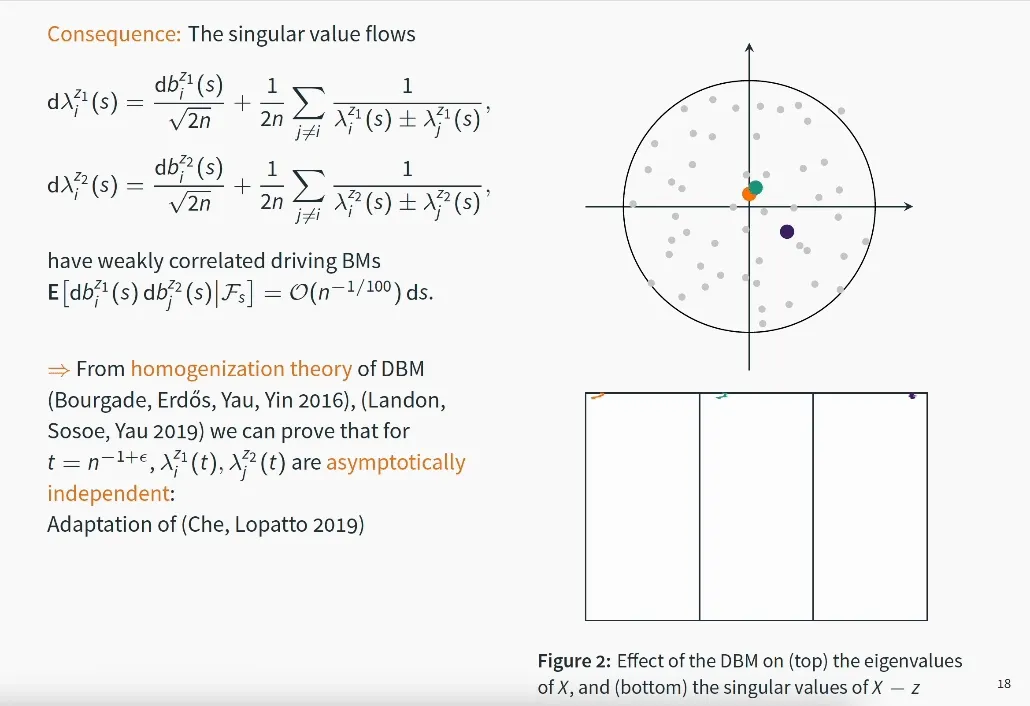
One key ingredient of the proof is the asymptotic independence of singular value flows for sufficiently distant spectral parameters after a short time:

Abstract

We consider large non-Hermitian random matrices X with complex, independent, identically distributed centred entries and show that the linear statistics of their eigenvalues are asymptotically Gaussian for test functions having 2+ϵ derivatives. Previously this result was known only for a few special cases; either the test functions were required to be analytic [Rider, Silverstein 2006], or the distribution of the matrix elements needed to be Gaussian [Rider, Virág 2007], or at least match the Gaussian up to the first four moments [Tao, Vu 2016; Kopel 2015]. We find the exact dependence of the limiting variance on the fourth cumulant that was not known before. The proof relies on two novel ingredients: (i) a local law for a product of two resolvents of the Hermitisation of X with different spectral parameters and (ii) a coupling of several weakly dependent Dyson Brownian Motions. These methods are also the key inputs for our analogous results on the linear eigenvalue statistics of real matrices X that are presented in the companion paper Cipolloni, Erdős, Schröder 2019.

Paper

1912.04100.pdf