Random matrices with slow correlation decay

Summary

We prove universality for a large class of random matrices with correlated entries. This very general result has been used numerous times, also in more applied research.

Main result

The first main result asserts that the resolvent $G(z):=(H-z)^{-1}$ of an $n\times n$ random matrix $H$ with correlated entries is well approximated by the unique solution $M(z)$ to the Matrix Dyson Equation

$$-M(z)^{-1} = \mathbf{E} (H-\mathbf E H) M(z) (H-\mathbf E H) + z - \mathbf E H.$$

The second main result is that the local eigenvalue statistics of $H$ are given by the universal Sine kernel statistics.

Proof

One key ingredient for the proof is the fast relaxation to equilibrium of Dyson Brownian motion:

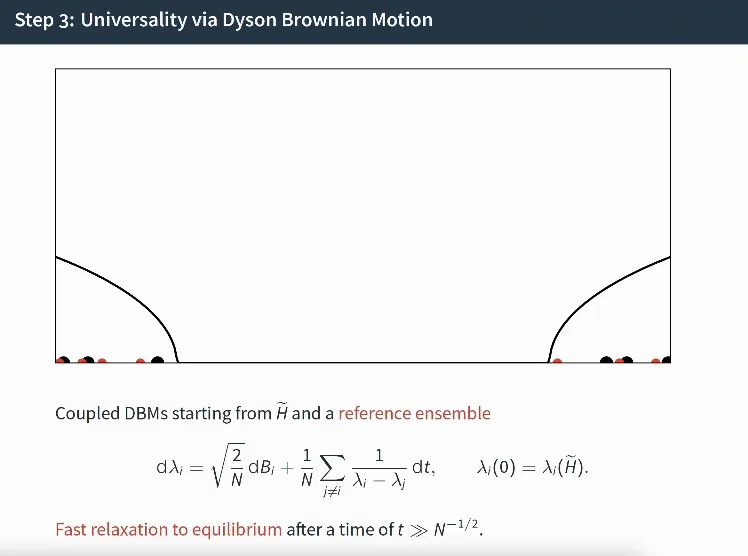
Here there are two classes of particles (red and black) which initially are independent from each other. Then both particles are evolved using the same DBM and already after a short time the trajectories merge.

Abstract

We consider large random matrices with a general slowly decaying correlation among its entries. We prove universality of the local eigenvalue statistics and optimal local laws for the resolvent away from the spectral edges, generalizing the recent result of arXiv:1604.08188 to allow slow correlation decay and arbitrary expectation. The main novel tool is a systematic diagrammatic control of a multivariate cumulant expansion.

Paper

1705.10661.pdf