Controlling Quadcopters using Ultra-wideband

The Automatic Control Laboratory (IfA) at ETH Zurich currently organizes a P&S course for Bachelor students on control of quadcopters. The system for this course currently uses Bitcraze’s Crazyflie 2.0 quadcopters with three reflective balls attached, which allows for precise localization with a Vicon camera system. However, this system is rather expensive and a hastle to set up. The IfA has also been working on ultra-wideband (UWB) localization, developing a robust system to locate a tag using only UWB ranging.

The aim of this group project was to combine the two other projects: locate and control the Crazyflie using only UWB and onboard sensors. While UWB is a lot less precise than the Vicon system, it is far more versatile and less expensive. Using an optimization-based approach, the location of the Crazyflie can be determined using only the distances between the Crazyflie and fixed anchors. As this information is quite flawed, the position has to be filtered and a controller optimized to work with this new method of localization.

The distance calculation between anchor and tag is based on a two-way communication where packets are sent between both devices and the travel time calculated. By using the known propagation speed of UWB-radio signals, one can calculate the distance. The method used in this project uses the concept of a (Double-sided) Two-Way-ranging, where 4 packets are exchanged for one single distance calculation.

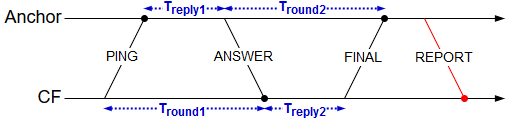
The tag starts by sending a PING packet and, upon receiving it, the anchor responds with an ANSWER packet. The tag finishes the ranging by sending a FINAL packet. At each step (upon receiving or sending a packet) each device locally saves the current imestamp. By calculating the time difference between two consecutive timestamps, it can get the absolute delta time of a single successful two-way communication. This gives rise to the four delta timestamps required to calculate the traveling time.

$$t_{prop}=\frac{t_{round1}\cdot t_{round2}-t_{reply1} \cdot t_{reply2}}{t_{round1}+t_{round2}+t_{reply1}+t_{reply2}}$$

Given all the distances to all six used anchor points, the next challenge is to, using the known anchor positions, calculate the Crazyflies‘s position. Many different methods exist to do this, but for the sake of this paper an optimization solver will be implemented. The problem to be solved can be formulated as a non-linear least-squares

$$\min{\sum_{i}^{N}(d_{i}^2-\|\mathbf{p}_i-\mathbf{p}_{CF}\|^2)^2}$$

where $d_i$ is the distance between anchor $i$ and the Crazyflie, $\mathbf{p}_i=[x_i,y_i,z_i]^T$ is the cartesian position of anchor $i$ and $\mathbf{p}_{CF}=[x_{CF},y_{CF},z_{CF}]^T$ is the Crazyflies`s position. Thus, $d_i$ and $\mathbf{p}_i$ are fixed parameters in this least squares problem, and the $\mathbf{p}_{CF}$ are the variables to be determined.

Considering the generalized formal definition of a least-squares, $$\min{\sum_{i}^{N}r_{i}^2},\,\,\,\,\, r_{i}=y_{i}-f(\mathbf{x_i},\boldsymbol{\beta})$$ $$m\,\mathrm{functions}\,\,\mathbf{r}=(r_1,...,r_m) \in \mathbb{R}^m$$ $$n\,\mathrm{variables}\,\,\boldsymbol{\beta}=(\beta_1,...,\beta_n) \in \mathbb{R}^n$$
where $\mathbf{x_i}$ is the independent variable and $y_{i}$ is the dependent variable. A standard algorithm for solving these kind of problems (also the method used to solve our problem) is the Gauss-Newton algorithm.