Chapter 6 Designs with multiple treatment factors

6.1 Introduction

The treatment design in our drug example contains a single treatment factor, and one of three drugs is administered to each mouse. Factorial treatment designs use several treatment factors, and a treatment administered to an experimental unit is then a combination of one level from each factor.

While we analyzed our tumor diameter example as a one-way ANOVA, we can alternatively interpret the experiments as a factorial design with two treatment factors: Drug with three levels ‘none’, ‘CP’, and ‘IFF’, and Inhibitor with two levels ‘none’ and ‘RTV’. Each of the six previous treatment levels is then a combination of one drug and absence/presence of RTV.

Factorial designs can be analyzed using a multi-way analysis of variance—a relatively straightforward extension from Chapter 4—and linear contrasts. A new phenomenon in these designs is the potential presence of interactions between two (or more) treatment factors. The difference between levels of the first treatment factor then depends on the level of the second treatment factor and greater care is required in the interpretation.

6.2 Experiment

In Chapter 4, we already suspected that the four drugs might show different effects under different diets, but ignored this aspect by using the same low-fat diet for all treatment groups. We now consider the diet again and expand our investigation by introducing a second diet with high fat content. We concentrate on drugs \(D1\) and \(D2\) from class A, since they were much superior than the two drugs from class B. Since we are no longer interested only in comparing the drugs, but also to establish if they show any effect at all, we introduce a control group using a placebo treatment with no active substance.

The proposed experiment is as follows: two drugs, \(D1\) and \(D2\), and one placebo treatment are given to 8 mice each, and treatment allocation is completely at random. For each drug, 4 mice are randomly selected and receive a low fat diet, while the other 4 mice receive a high fat diet. The treatment design then consists of two treatment factors, Drug and Diet, with three and two levels, respectively. Since each drug is combined with each diet, the two treatment factors are crossed, and the design is balanced because each drug-diet combination is allocated to the same number of mice.

A crucial point in this experiment is the independent and random assignment of combinations of treatment factor levels to each mouse. We have to be careful not to break this independent assignment in the implementation of the experiment. If the experiment requires multiple cages, for example, it is very convenient to feed the same diet to all mice in a cage. This is not a valid implementation of the experimental design, however, because the diet is now randomized on cages and not on mice, and this additional structure is not reflected in the design.

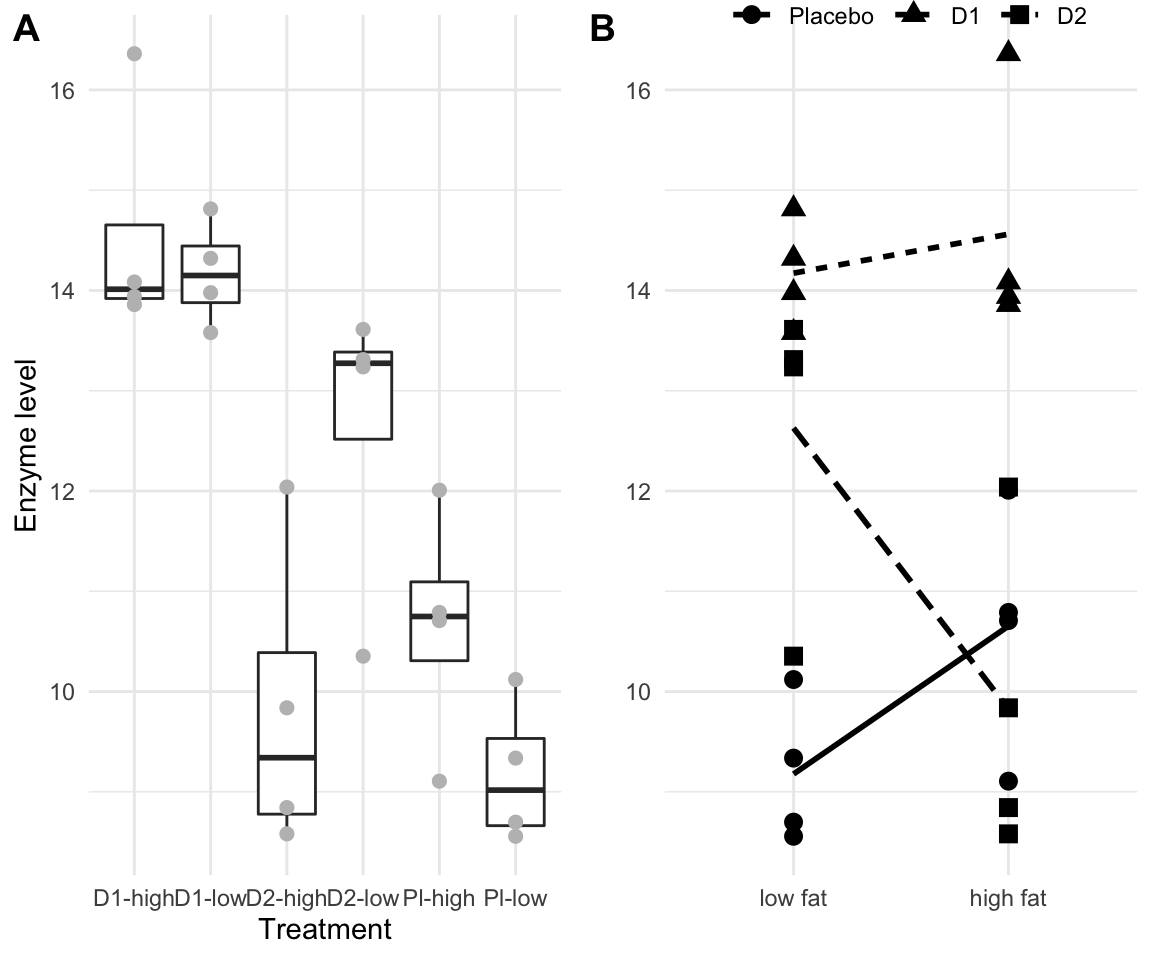
Figure 6.1: A: Enzyme levels for combinations of three drugs and two diets, four mice each in a completely randomized design with two-way crossed treatment structure. Points are the response values, boxplots show summary for each treatment group. B: same data as interaction plot, with shape indicating drug treatment, and lines connecting the average response values for each drug over diets.

Table 6.1: Enzyme levels for combinations of three drugs and two diets, four mice per combination.

	low fat				high fat
	1	2	3	4	1	2	3	4
Placebo	10.12	8.56	9.34	8.70	10.79	12.01	9.11	10.71
D1	14.32	13.58	14.81	13.98	14.08	13.86	13.94	16.36
D2	13.61	13.24	10.35	13.31	9.84	8.84	12.04	8.58

Data

The 24 measured enzyme levels for the six treatment combinations are shown in Table 6.1 and Figure 6.1(A). A useful alternative visualization is an interaction plot as shown in Figure 6.1(B), where we use the levels of Diet for the \(x\)-axis, the enzyme levels for the \(y\)-axis, and the levels of Drug are represented by point shape. We also show the average response in each of the six treatment groups and connect those of the same drug by a line, linetype indicating the drug.

Even a cursory glance reveals that both drugs have an effect on the enzyme level, resulting in higher observed enzyme levels compared to the placebo treatment on a low fat diet. Two drug treatments—\(D1\) and placebo—appear to have increased enzyme levels under a high-fat diet, while levels are lower under a high-fat diet for \(D2\). This is an indication that the effect of the diet is not the same for the three drug treatments and there is thus an interaction between drug and diet.

Hasse diagrams

The treatment structure of this experiment is shown in Figure 6.2 (left) and is a factorial treatment design with two crossed treatment factors Drug and Diet, which we write next to each other in the treatment structure diagram. Each treatment combination is a level of the new interaction factor Drug:Diet, nested in both treatment factors.

The unit structure only contains the single unit factor (Mouse), as shown in Figure 6.2 (center).

We derive the experiment structure by determining the experimental unit for each treatment factor: both Drug and Diet are randomly assigned to (Mouse), and so is therefore each combination as a level of Drug:Diet. We therefore draw an edge from Drug:Diet to (Mouse). The two potential edges from Drug and Diet to (Mouse) are redundant and we omit them, yielding the diagram in Figure 6.2 (right).

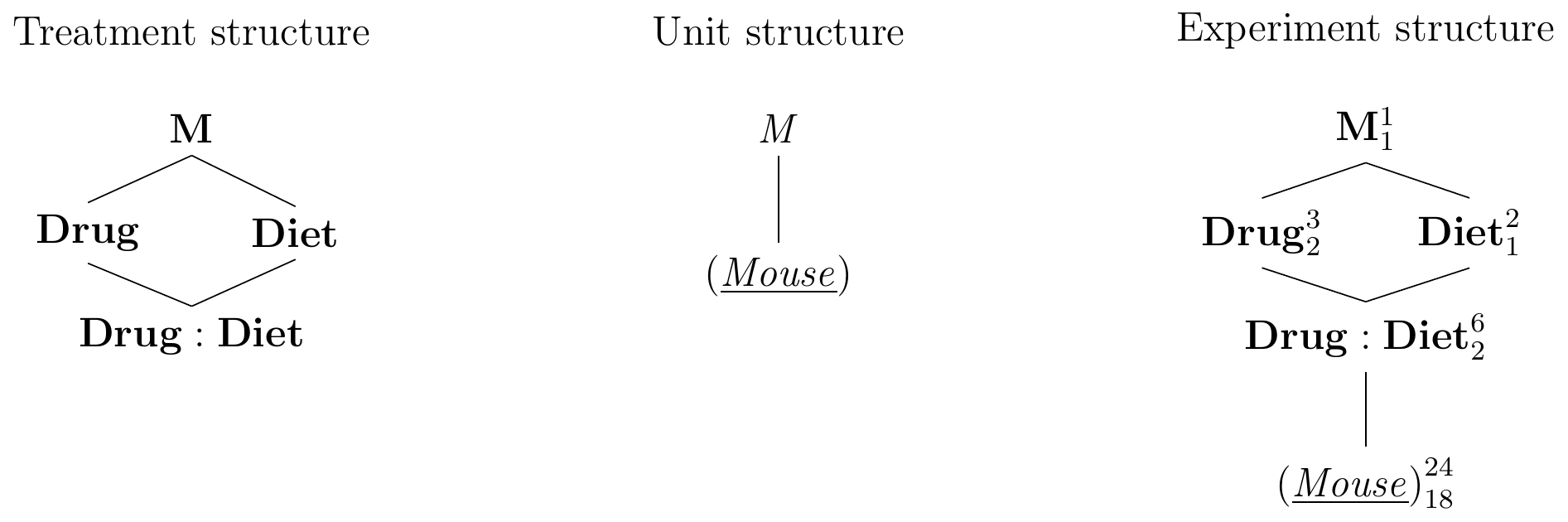
Figure 6.2: Completely randomized design for determining effect of two different drugs and placebo on two different diets using four mice per drug and a single response measurement per mouse.

6.3 Two-way ANOVA

The analysis of variance framework readily extends to more than one treatment factor. Already with two factors, we find all the new properties of this extension and we focus our detailed discussion on this case.

6.3.1 Linear model

For our general discussion, we consider two treatment factors A with \(a\) levels and B with \(b\) levels; the interaction factor A:B then has \(a\cdot b\) levels. We again denote by \(n\) the number of experimental units for each treatment combination in a balanced design, and by \(N=a\cdot b\cdot n\) the total sample size. For our example \(a=3\), \(b=2\), \(n=4\), and thus \(N=24\).

Cell means model

A simple linear model is the cell means model \[ y_{ijk} = \mu_{ij} + e_{ijk}\;, \] in which each cell mean \(\mu_{ij}\) is the average response of the experimental units receiving level \(i\) of the first treatment factor and level \(j\) of the second treatment factor and \(e_{ijk}\sim N(0,\sigma_e^2)\) is the residual of the \(k\)th replicate for the treatment combination \((i,j)\).

Our example leads to \(3\times 2=6\) cell means \(\mu_{11},\dots,\mu_{32}\); the cell mean \(\mu_{11}\) is the average response to the placebo treatment under the low-fat diet, and \(\mu_{32}\) is the average response to the \(D2\) drug treatment under the high-fat diet.

The cell means model does not explicitly reflect the factorial treatment design, and we could analyze our experiment as a one-way ANOVA with six treatment levels.

Parametric model

The parametric model \[ y_{ijk} = \mu + \underbrace{(\mu_{i\bullet}-\mu)}_{\alpha_i} + \underbrace{(\mu_{\bullet j}-\mu)}_{\beta_j} + \underbrace{(\mu_{ij}-\mu_{i\bullet}-\mu_{\bullet j}+\mu)}_{(\alpha\beta)_{ij}} + e_{ijk}\;, \] makes the factorial treatment design explicit. Each cell mean \(\mu_{ij}\) is decomposed into four contributions: a general mean \(\mu\), the average cell mean \(\mu_{i\bullet}\) for level \(i\) of A (averaged over all levels of B), the average cell mean \(\mu_{\bullet j}\) for level \(j\) of B (averaged over all levels of A), and an interaction for each level of A:B.

The model components are shown schematically in Figure 6.3 (A) for our drug-diet example. Each drug corresponds to a row, and \(\mu_{i\bullet}\) is the average response for drug \(i\), where the average is taken over both diets in row \(i\). Each diet corresponds to a column, and \(\mu_{\cdot j}\) is the average response for column \(j\) (over the three drugs). The interaction is the difference between the additive effect of the row and column differences to the grand mean \(\mu_{i\bullet}-\mu_{\bullet\bullet}\) and \(\mu_{\bullet j}-\mu_{\bullet\bullet}\), and the actual cell mean’s difference \(\mu_{ij}-\mu_{\bullet\bullet}\) from the grand mean: \[ \mu_{ij}-\mu_{i\bullet}-\mu_{\bullet j}+\mu = (\mu_{ij}-\mu) \,-\, \left((\mu_{i\bullet}-\mu) \,+\, (\mu_{\bullet j}-\mu)\right)\;. \]

The model has five sets of parameters: \(a\) parameters \(\alpha_i\) and \(b\) parameters \(\beta_j\) constitute the main effect parameters of factor A and B, respectively, while the \(a\cdot b\) parameter \((\alpha\beta)_{ij}\) are the interaction effect parameters of factor A:B. They correspond to the factors in the experiment diagram: in our example, the factor M is associated by the grand mean \(\mu\), while the two treatment factors Drug and Diet are associated with \(\alpha_i\) and \(\beta_j\), respectively, and the interaction factor Drug:Diet with \((\alpha\beta)_{ij}\). The unit factor (Mouse) has 24 levels, each reflecting the deviation of a specific mouse, and is represented by the residuals \(e_{ijk}\) and their variance \(\sigma_e^2\). The degrees of freedom are the number of independent estimates for each set of parameters.

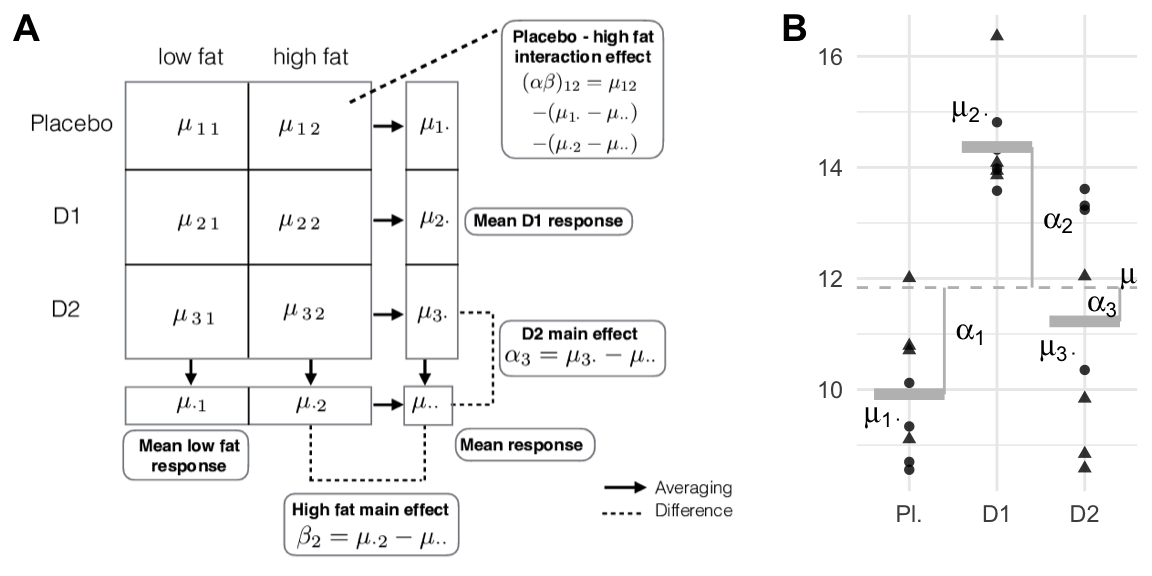
Figure 6.3: A: The 3-by-2 data table with averages per treatment. Main effects are differences between row- or column means and grand mean. Interaction effects are differences between cell means and the two main effects. B: marginal data considered for drug-only merges data for each drug over diets. The three averages correspond to the row means and point shapes correspond to diet. Dashed line: grand mean; solid grey lines: group means; vertical lines: group mean deviations.

6.3.2 Analysis of Variance

The analysis of variance with more than one treatment factor is a direct extension of the one-way ANOVA, and is again based on decomposing sums of squares and degrees of freedom. Each treatment factor can be tested individually using a corresponding \(F\)-test.

6.3.2.1 Sums of squares

For balanced designs, we decompose the sum of squares into one part for each factor in the design. The total sum of squares is \[ \text{SS}_\text{tot} = \text{SS}_\text{A} + \text{SS}_\text{B} + \text{SS}_\text{AB} + \text{SS}_\text{res} = \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^n(y_{ijk}-\bar{y}_{\cdot\cdot\cdot})^2\;, \] and measures the overall variation between the observed values and the grand mean. We now have two treatment sum of squares, one for factor A and one for B; they are the squared differences of the group mean from the grand mean: \[ \text{SS}_\text{A} = \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^n(\bar{y}_{i\bullet\bullet}-\bar{y}_{\bullet\bullet\bullet})^2 = bn\sum_{i=1}^a(\bar{y}_{i\bullet\bullet}-\bar{y}_{\bullet\bullet\bullet})^2 \;\text{and}\; \text{SS}_\text{B} = an\sum_{j=1}^b(\bar{y}_{\bullet j\bullet}-\bar{y}_{\bullet\bullet\bullet})^2\;. \] Each treatment sum of squares is found by lumping together the data over all levels of the other treatment factor. For example, \(\text{SS}_{\text{drug}}\) in our example is based on lumping data over the diet treatment levels, corresponding to a one-way ANOVA situation as in Figure 6.3 (B).

The interaction sum of squares for A:B is \[ \text{SS}_\text{AB} = n\sum_{i=1}^a\sum_{j=1}^b(\bar{y}_{ij\cdot}-\bar{y}_{i\bullet\bullet}-\bar{y}_{\bullet j\bullet}+\bar{y}_{\bullet\bullet\bullet})^2\;. \] If interactions exist, parts of \(\text{SS}_\text{tot}-\text{SS}_\text{A}-\text{SS}_\text{B}\) are due to a systematic difference between the additive prediction for each group mean, and the actual mean of that treatment combination.

The residual sum of squares measure the distances of each response to its corresponding treatment mean: \[ \text{SS}_\text{res} = \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^n(y_{ijk}-\bar{y}_{ij\bullet})^2\;. \] For our example, we find \(\text{SS}_\text{tot}=\) 129.44 decomposed into treatments \(\text{SS}_\text{A}=\) 83.73 and \(\text{SS}_\text{B}=\) 0.59, interaction \(\text{SS}_\text{drug:diet}=\) 19.78 and residual \(\text{SS}_\text{res}=\) 25.34 sum of squares.

6.3.2.2 Degrees of freedom

The degrees of freedom also partition by the corresponding factors, and the rules for Hasse diagrams allow quick and easy calculation. For the general two-way ANOVA, we have \[ \text{df}_\text{tot} = abn-1 = \text{df}_\text{A} + \text{df}_\text{B} + \text{df}_\text{AB} + \text{df}_\text{res} = (a-1) + (b-1) + (a-1)(b-1) + ab(n-1)\;. \] With \(a=3\), \(b=2\), \(n=4\) for our example, we find \(\text{df}_\text{A}=\) 2, \(\text{df}_\text{B}=\) 1, \(\text{df}_\text{AB}=\) 2, and \(\text{df}_\text{res}=\) 18.

6.3.2.3 Mean squares

Mean squares are found by dividing the sum of squares terms by their degrees of freedom. For example, we can calculate the total mean squares \[ \text{MS}_\text{tot} = \frac{\text{SS}_\text{tot}}{abn-1}\;, \] which corresponds to the variance in the data ignoring treatment groups. Further, \[ \text{MS}_\text{A} = \text{SS}_\text{A}/ \text{df}_\text{A}\,, \; \text{MS}_\text{B} = \text{SS}_\text{B} / \text{df}_\text{B}\,, \; \text{MS}_\text{AB} = \text{SS}_\text{AB} / \text{df}_\text{AB}\,,\; \text{MS}_\text{res} = \text{SS}_\text{res} / \text{df}_\text{res}\;. \] In our example, \(\text{MS}_\text{A}=\) 41.87, \(\text{MS}_\text{B}=\) 0.59, \(\text{MS}_\text{AB}=\) 9.89, and \(\text{MS}_\text{res}=\) 1.41.

6.3.2.4 \(F\)-tests

We can perform an omnibus \(F\)-test for each factor by comparing its mean squares with the corresponding residual mean squares. With a completely randomized design, all treatment factors are randomly allocated to the same unit factor ((Mouse) in our example), and the denominator for the \(F\)-statistic is idential for all tests.

For example, the hypothesis that the average response values for each level of A are identical is \[ H_0: \mu_{1\bullet}=\cdots=\mu_{a\bullet} \] and we test it using the \(F\)-statistic \[ F = \frac{\text{MS}_\text{A}}{\text{MS}_\text{res}}\sim F_{a-1,ab(n-1)}\;. \] The arguments are exactly the same as before: the mean square of A has expectation \[ \mathbb{E}(\text{MS}_\text{A}) = \sigma_e^2 + \frac{nb}{a-1}\sum_{i=1}^a\alpha_i^2\;, \] and \(\text{MS}_\text{A}\) provides a second independent estimate of \(\sigma_e^2\) if the null hypothesis is true. Similarly, the expectations for the two other factors are \[ \mathbb{E}(\text{MS}_\text{B}) = \sigma_e^2 + \frac{na}{b-1}\sum_{j=1}^b\beta_j^2 \quad\text{and}\quad \mathbb{E}(\text{MS}_\text{AB}) = \sigma_e^2 + \frac{n}{(a-1)(b-1)} \sum_{i=1}^a\sum_{j=1}^b (\alpha\beta)_{ij}^2\;, \] and both are independent estimates of the residual variance if the respective null hypotheses are true. The corresponding test statistics for B and A:B are \[ F = \frac{\text{MS}_\text{B}}{\text{MS}_\text{res}} \sim F_{b-1,ab(n-1)}\,,\quad\text{and}\quad F = \frac{\text{MS}_\text{AB}}{\text{MS}_\text{res}} \sim F_{(a-1)(b-1),ab(n-1)}\;. \] We find the correct denominator mean squares from the experiment structure diagram: it corresponds to the closest random factor below the corresponding treatment factor and is \(\text{MS}_\text{res}\) for all three tests, corresponding to the unit factor (Mouse) in our example.

6.3.2.5 ANOVA table

Using R, all of these calculations are done easily using aov(). We find the model specification from the Hasse diagrams. All fixed factors are in the treatment structure and provide the terms 1+drug+diet+drug:diet which we abbreviate as drug*diet. All random factors are in the unit structure, providing Error(mouse), which we may drop from the specification since (Mouse) is the lowest random unit factor. The ANOVA yields

m = aov(y~drug*diet, data=d)
summary(m)

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
drug	2	83.73	41.87	29.74	1.973e-06
diet	1	0.5883	0.5883	0.4179	0.5262
drug:diet	2	19.78	9.89	7.025	0.00556
Residuals	18	25.34	1.408

We find that the sums of squares for the drug effect are large compared to all other contributors and Drug is highly significant. The Diet main effect does not achieve significance at any reasonable level, and its sums of squares are tiny. However, we find a large and significant Drug:Diet interaction and must therefore be very careful in our interpretation of the results as we discuss next.

6.3.3 Interpretation of main effects

The main effect of a treatment factor is the deviation between group means of its factor levels, averaged over the levels of all other treatment factors.

In our example, the null hypothesis of the drug main effect is \[ H_0(\text{drug}):\;\mu_{1\bullet}=\mu_{2\bullet}=\mu_{3\bullet}=\mu \;\;\text{or equiv.}\;\; H_0(\text{drug}):\;\alpha_1=\alpha_2=\alpha_3=0\;, \] and the corresponding hypothesis for the diet main effect is \[ H_0(\text{diet}):\;\mu_{\bullet 1}=\mu_{\bullet 2}=\mu \;\;\text{or equiv.}\;\; H_0(\text{diet}):\;\beta_1=\beta_2=\beta_3=0\;, \] The first hypothesis asks if there is a difference in the enzyme levels between the three drugs, ignoring the diet treatment by averaging the obervations for low fat and high fat diet for each drug. The second hypothesis asks if there is a difference between enzyme levels for the two diets, averaged over the three drugs.

From the ANOVA table, we see that the main effect of the drug treatment is highly significant, indicating that regardless of the diet, the drugs affect enzyme levels differently. In contrast, the diet main effect is negligibly small with a large \(p\)-value, but the raw data in Figure 6.1(A) shows that while the diet has no influence on the drug levels when averaged over all drug treatments, it has visible effects for some drugs: the effect of \(D1\) seems to be unaffected by the diet, while a low fat diet yields higher enzyme levels for \(D2\), but lower levels for placebo.

6.3.4 Interpretation of interactions

The interaction effects quantify how different the effect of one factor is for different levels of another factor. For our example, the large and significant interaction factor shows that while the diet main effect is negligible, the two diets have very different effect depending on the drug treatment. Simply because the diet main effect is not significant therefore does not mean that the diet effect can be neglected for each drug. The most important rule when analyzing designs with factorial treatment structures is therefore:

Be careful when interpreting main effects in the presence of large interactions.

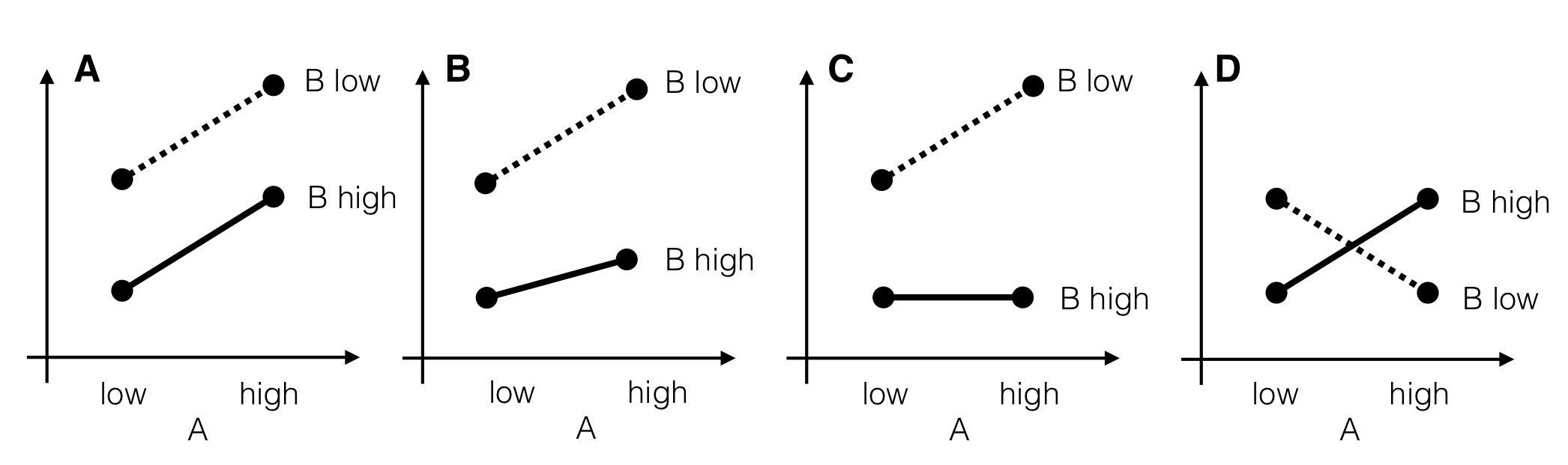
Figure 6.4: Four stylized scenarios with different interactions. A: parallel lines indicate no interaction and an additive model. B: small interaction and nonzero main effects. Factor B attenuates effect of factor A. C: strongly pronounced interaction. Factor B on high level completely compensates effect of factor A. D: complete effect reversal with both main effects zero. All the information about factor effects is in the interaction.

Four illustrative examples of interactions are shown in Figure 6.4 for two factors A and B with two levels each. In each panel, the two levels of A are shown on the horizontal axis, and a response on the vertical axis. The two lines connect the same levels of factor B between levels of A.

In the first case (Fig. 6.4(A)), the two lines are parallel and the difference in response between the low to the high levels of B are the same for both levels of A, and vice-versa. The average responses \(\mu_{ij}\) in each of the four treatment groups are then fully described by an additive model \[ \mu_{ij} = \mu + \alpha_i + \beta_j + e_{ijk}\;, \] with no interaction and \((\alpha\beta)_{ij}=0\).

In our example, we might compare the responses to placebo and drug \(D1\) between diets. While the corresponding estimated lines in Figure 6.1(B) are not exactly parallel, this could potentially be explained by random fluctuations. In this case, the two cell means \(\mu_{11}\) for placebo and \(\mu_{21}\) for \(D1\) under a low fat diet are \[ \mu_{11} = \mu+\alpha_1+\beta_1 \quad\text{and}\quad \mu_{21} = \mu+\alpha_2+\beta_1\;, \] and their difference is \(\mu_{21}-\mu_{11}=\alpha_2-\alpha_1\). Under a high fat diet, the cell means are \[ \mu_{12} = \mu+\alpha_1+\beta_2 \quad\text{and}\quad \mu_{22} = \mu+\alpha_2+\beta_2 \;, \] and their difference is \(\mu_{22}-\mu_{12}=\alpha_2-\alpha_1\). In other words, the difference between the two drugs is independent of the diet and conversely the difference between the two diets is independent of the drug administered. We can then interpret the drug effect without regard for the diet and speak of a “drug main effect” or conversely interpret the diet effect independently of the drug and speak of a “diet main effect”.

It might also be that the true situation for placebo and \(D1\) is more similar to Figure 6.4(B), a quantitative interaction: the increase in response from high to low level for factor B is more pronounced if A is on the high level, yet we achieve higher responses for B low under any level of A, and conversely a higher response is achieved by using A on the high level for both levels of B. Then, the effects of treatments A and B are not simply additive, and the interaction term \[ (\alpha\beta)_{ij} = \mu_{ij} - (\mu+\alpha_i+\beta_j) \] quantifies exactly how much the observed cell mean \(\mu_{ij}\) differs from the value predicted by the additive model \(\mu+\alpha_i+\beta_j\).

For our example, the responses to placebo and drug \(D1\) under a low fat diet are then \[ \mu_{11} = \mu+\alpha_1+\beta_1+(\alpha\beta)_{11} \quad\text{and}\quad \mu_{21} = \mu+\alpha_2+\beta_1 +(\alpha\beta)_{21}\;, \] and thus the difference is \(\mu_{21}-\mu_{11}=(\alpha_2-\alpha_1)+((\alpha\beta)_{21}-(\alpha\beta)_{11})\), while for the high fat diet, we find a difference between placebo and \(D1\) of \(\mu_{22}-\mu_{12}=(\alpha_2-\alpha_1)+((\alpha\beta)_{22}-(\alpha\beta)_{12})\). If at least one of the parameters \((\alpha\beta)_{ij}\) are not zero, then the difference between \(D1\) and placebo depends on the diet. The interaction is the difference of differences \[ \underbrace{(\mu_{21}-\mu_{11})}_{\text{low fat}} - \underbrace{(\mu_{22}-\mu_{12})}_{\text{high fat}} = \left(\,(\alpha\beta)_{21}-(\alpha\beta)_{11}\,\right) - \left(\,(\alpha\beta)_{22}-(\alpha\beta)_{12}\,\right)\;, \] and is fully described by the four interaction parameters corresponding to the four cell means involved.

It is then misleading to speak of a “drug main effect”, since this effect is diet-dependent. In our case of a quantitative interaction, we find that a placebo treatment always gives lower enzyme levels, independent of the diet. The diet only modulates this effect, and we can achieve a greater increase in enzyme levels for \(D1\) over placebo if we additionally use a low fat diet.

The interaction becomes more pronounces the more “non-parallel” the line become. The interaction in Figure 6.4(C) is still quantitative and a low level of B always yields the higher response, but the modulation by A is much stronger than before. In particular, A has no effect under a high level of B and using either a low or high level yields the same average response, while under a low level of B, using a high level for A yields even higher responses. Note that there is an additional quantitative interaction between diet and \(D1\)/\(D2\), with \(D1\) consistently giving higher enzyme levels than \(D2\) under both diets. However, if we would only consider a low fat diet, then the small difference between responses to \(D1\) and \(D2\) might make us prefer \(D2\) if it is much cheaper or has a better safety profile, for example, while \(D2\) is no option under a high fat diet.

Interactions can also be qualitative, in which case we might see an effect reversal. Now, one level of B is no longer universally superior under all levels of A, as shown in Figure 6.4(D) for an extreme case. If A is on the low level, then higher responses are gained if B is on the low level, while for A on its high level, the high level of B gives higher responses.

We find this situation in our example when comparing the placebo treatment and \(D2\): under a low fat diet, \(D2\) shows higher enzyme levels, while enzyme levels are similar or even lower for \(D2\) than placebo under a high fat diet. In other words, \(D1\) is always superior to a placebo and we can universally recommend its use, we should only use \(D2\) for a low fat diet since it seems to have little to no (or even negative) effect under a high fat diet.

6.3.5 Effect sizes

We measure the effect size of each factor using its \(f^2\) value. For our generic two-factor design with factors A and B with \(a\) and \(b\) levels, respectively, the effect sizes are \[ f^2_\text{A} = \frac{1}{a\sigma_e^2}\sum_{i=1}^a \alpha_i^2 \,, \quad f^2_\text{B} = \frac{1}{b\sigma_e^2}\sum_{j=1}^b \beta_j^2 \,, \quad f^2_\text{A:B} = \frac{1}{ab\sigma_e^2}\sum_{i=1}^a\sum_{j=1}^b (\alpha\beta)_{ij}^2 \,, \] respectively, which in our example are \(f^2_\text{drug}=\) 0.43 (huge), \(f^2_\text{diet}=\) 0.02 (tiny), and \(f^2_\text{drug:diet}=\) 0.3 (medium).

Alternatively, we can measure the effect of factor X by its variance explained \(\eta^2_\text{X}=\text{SS}_\text{X}/\text{SS}_\text{tot}\), which in our example yields \(\eta^2_\text{drug}=\text{SS}_\text{drug}/\text{SS}_\text{tot} =\) 65% for the drug main effect, \(\eta^2_\text{diet}=\) 0.45% for the diet main effect, and \(\eta^2_\text{drug:diet}=\) 15% for the interaction. This effect size measure has two caveats for multi-way ANOVAs, however. First, the total sum of squares contains all those parts of the variation ‘explained’ by the other treatment factors. The magnitude of any \(\eta^2_\text{X}\) therefore depends on the number of other treatment factors, and on the proportion of variation explained by them. The second caveat is a consequence of this: the explained variance \(\eta^2_{X}\) does not have a simple relationship with the effect size \(f^2_{X}\), which compares the variation due to the factor alone to the residual variance and excludes all effects due to other treatment factors.

We resolve both issues by the partial-\(\eta^2\) effect size measure, which is the fraction of variation explained by each factor over the variation that remains to be explained after accounting for all other treatment factors: \[ \eta^2_\text{p, A} = \frac{\text{SS}_\text{A}}{\text{SS}_\text{A}+\text{SS}_\text{res}}\,, \quad \eta^2_\text{p, B} = \frac{\text{SS}_\text{B}}{\text{SS}_\text{B}+\text{SS}_\text{res}}\,, \quad \eta^2_\text{p, A:B} = \frac{\text{SS}_\text{A:B}}{\text{SS}_\text{A:B}+\text{SS}_\text{res}}\,. \] Note that \(\eta_\text{p, X}^2=\eta_\text{X}^2\) for a one-way ANOVA. The partial-\(\eta^2\) are not a partition of the variation into single factor contributions and therefore do not sum to one, but they have a direct relation to \(f^2\): \[ f^2_\text{X} = \frac{\eta^2_\text{p, X}}{1-\eta^2_\text{p, X}} \] for any treatment factor X. In our example, we find \(\eta^2_\text{p, drug}=\) 77%, \(\eta^2_\text{p, diet}=\) 2%, and \(\eta^2_\text{p, drug:diet}=\) 44%.

6.3.6 Model reduction and marginality principle

In the one-way ANOVA, the omnibus \(F\)-test was of limited use for addressing our scientific questions. With more factors in the experiment design, however, a non-significant \(F\)-test and a small effect size would allow us to remove the corresponding factor from the model. This is known as model reduction, and the reduced model is often easier to analyze and to interpret.

In order to arrive at an interpretable reduced model, we need to take account of the principle of marginality for model reduction (Nelder 1994):

If we remove a factor from the model, then we also need to remove all interaction factors involving this factor.

For a two-way ANOVA, the marginality principle implies that only the interaction factor can be removed in the first step. We then re-estimate the resulting additive model and might further remove one or both main effects factors if their effects are small and non-significant. If the interacition factor is significant or its effect size is deemed too large, then the two-way ANOVA model cannot be reduced.

In our example, we find that Diet has a non-significant \(p\)-value and a low effect size \(\eta^2_\text{diet}\), which suggests that it does not have an appreciable main effect when averaged over all drugs. However, Diet is involved in the significant interaction factor Drug:Diet with large effect size, and the marginality principle prohibits removing Diet from the model. The interpretation of the model would suffer severely if we removed Diet but kept Drug:Diet. The resulting model would be of the form \[ y_{ijk} = \mu + \alpha_i + (\alpha\beta)_{ij} + e_{ijk}\;. \] It has three sets of parameters: the grand mean, one deviation for each level of A, and additionally different and independent deviations for the levels of B within each level of A. This model thus describes B as nested in A, in contrast to the actual design which has A and B crossed. This violation is easily seen if we compare the resulting experiment diagram in Figure 6.5 (right) to the diagram of the original design in Figure 6.5 (left) and recall that two nested factors correspond to a main effect and an interaction effect since A/B=A+A:B.

Figure 6.5: Left: Experiment structure diagram for full two-way model with interaction. Factors A and B are crossed. Right: Experiment structure resulting from removing one treatment factor but not its interaction, violating the marginality principle. Factor B is now nested in A.

Table 6.2: Empirical means (Data), and predicted means for each cell for full model with interaction (Full), additive model without interactions (Additive), one-way model containing only main effect for drug (Drug only), respectively diet (Diet only), and trivial model with no treatment factors (Average).

Drug	Diet	Data	Full	Additive	Drug only	Diet only	Average
Placebo	low fat	9.18	9.18	10.07	9.92	11.99	11.84
D1	low fat	14.17	14.17	14.52	14.37	11.99	11.84
D2	low fat	12.63	12.63	11.38	11.23	11.99	11.84
Placebo	high fat	10.65	10.65	9.76	9.92	11.68	11.84
D1	high fat	14.56	14.56	14.21	14.37	11.68	11.84
D2	high fat	9.83	9.83	11.07	11.23	11.68	11.84

Illustration by model predictions

There are five possible linear models for our design with two crossed treatment factors. Their model predictions for the six cell means are shown in Table 6.2. The first two columns show the levels of the two treatment factors, while the third column corresponds to the empirical averages calculated from the four observations for each treatment group. The following five columns are the predicted cell means for the following models:

• Full is the linear model with both main effects and interaction term; the specification is y~1+drug+diet+drug:diet with predicted cell means \(\mu_{ij} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij}\). Since this model correctly specifies each cell mean as a sum of three treatment factor contributions, its predictions are in full agreement with the empirical cell means; this is typically not the case for real data.
• Additive contains both main effects but no interaction and has specification y~1+drug+diet. The predicted cell means \(\mu_{ij}=\mu+\alpha_i+\beta_j\) have identical differences between two levels of one factor, regardless of the level of the other factor. For example, this model states that the difference in enzyme levels between \(D1\) and placebo is -4.45 for a low fat diet and -4.45 for a high fat diet. This model would be appropriate if the interaction factor is non-significant and small, while both main effect factors are large or significant.
• Drug only further reduces the treatment structure by removing the interaction and the diet main effect, resulting in y~1+drug and cell means \(\mu_{ij}=\mu+\alpha_i\). It gives identical cell means for all conditions with the same drug, regardless of the diet applied. This model thus describes an experiment where the diet has no discernible effect on the enzyme levels, neither averaged over all drugs (no diet main effect) nor for any specific drug (no drug-diet interaction).
• Diet only is the respective model containing only a diet main effect, resulting in y~1+diet and \(\mu_{ij}=\mu+\beta_j\), and gives identical cell mean predictions for all drugs under a low fat diet, for example.
• Average is the most simple model containing only a general mean with y~1 and six identical cell means \(\mu_{ij}=\mu\).

6.3.7 A real-life example – continued

In Section 5.3, we looked into a real-life example and examined the effect of two anticancer drugs (IFF and CP) and an inhibitor (RTV) on tumor growth. We analysed the data using a one-way ANOVA based on six treatment groups and concentrated on relevant contrasts. There is, however, more structure in the treatment design, since we are actually looking at combinations of an anticancer drug and an inhibitor. To account for this structure, we reformulate the analysis to a more natural two-way ANOVA with two treatment factors: Drug with the three levels none, CP, and IFF, and Inhibitor with two levels none and RTV. Each drug is used with and without inhibitor, leading to a fully-crossed factorial treatment design with the two factors and their interaction Drug:Inhibitor. We already used the two conditions (none,none) and (none,RTV) as our control conditions in the contrasts analysis. The model specification is Diameter~Drug*Inhibitor and leads to the ANOVA table

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
Drug	2	495985	247993	235.1	4.109e-29
Inhibitor	1	238534	238534	226.1	5.128e-22
Drug:Inhibitor	2	80686	40343	38.24	1.963e-11
Residuals	60	63303	1055

We note that the previous sums of squares for Condition was 8.15204910^{5} in our one-way analysis and is now exactly partitioned into the contributions of our three treatment factors. The previous effect size of 93% is also partitioned into \(\eta^2_{\text{Drug}}=\) 56%, \(\eta^2_{\text{Inhibitor}}=\) 27%, and \(\eta^2_{\text{Drug:Inhibitor}}=\) 9%. In other words, the differences between conditions are largely caused by differences between the anticancer drugs, but the presence of the inhibitor also explains more than one-quarter of the variation. The interaction is highly significant and cannot be ignored, but its effect is much smaller compared to the two main effects. All of this is of course in complete agreement with our previous contrast analysis.

6.4 General factorial designs

We briefly discuss the general advantages of factorial treatment designs and extend our discussion to more than two treatment factors.

6.4.1 Advantage of factorial treatment design

Before the advantages of simultaneously using multiple crossed treatment factors in a factorial designs were fully understood by practitioners, so-called one variable at a time (OVAT) designs were commonly used for studying the effect of multiple treatment factors. Here, only a single treatment factor was considered in each experiment, while all other treatment factors were kept at a fixed level to achieve maximally controlled condition for studying each factor. These designs do not allow estimation of interactions and can therefore lead to incorrect interpretation if interactions are present. In contrast, factorial designs reveal interaction effects if they are present and provide the basis for correct interpretation of the experimental effects. The mistaken logic of OVAT designs was clearly recognized by R. A. Fisher in the 1920s:

No aphorism is more frequently repeated in connection with field trials, than that we must ask Nature few questions, or, ideally, one question, at a time. The writer is convinced that this view is wholly mistaken. Nature, he suggests, will best respond to a logical and carefully thought out questionnaire; indeed, if we ask her a single question, she will often refuse to answer until some other topic has been discussed. (Fisher 1926)

Slightly less obvious is the fact that factorial designs also require smaller sample sizes than OVAT designs, even if no interactions are present between the treatment factors. For illustration, we consider an experiment with two treatment factors A and B with two levels each and \(n\) observations for each of the four treatment level combinations. If the interaction A:B is large, then only a factorial design will allow correct inferences. If the interaction is negligible, then we have two estimates of the A main effect: first for B on the low level by contrasting the \(n\) observations for A on a low level with those \(n\) for A on a high level, and second for the \(n+n\) observations for B on a high level. The A main effect estimate is then the average of these two, based on the full \(4n\) observations. The same argument holds for estimating the B main effect. Since we need to estimate one general mean and one independent group mean each for A and B, the residual degrees of freedom are \(4n-3\).

In contrast, estimating the A and B main effects using an OVAT design of the same overall size of \(4n\) experimental units only provides \(2n\) units for each of the two experiments, and each main effect is estimated with \(2n-2\) residual degrees of freedom. With the same experimental resources, the resulting estimates are less precise and tests less powerful than the corresponding factorial design.

6.4.2 One observation per cell

Constraints on resources or complicated logistics for the experiment sometimes do not permit replication within each experimental condition, and we then have a single observation for each treatment combination. The Hasse diagram in Figure 6.6(left) shows the resulting experiment structure for two generic factors A and B with \(a\) and \(b\) levels, respectively, and one observation per combination. We do not have degrees of freedom for estimating the residual variance, and we can neither estimate confidence intervals for establishing the precision of estimates nor perform hypothesis tests. If large interactions are suspected, then this design is fundamentally flawed, and no simple statistical analysis can salvage this experiment.

The experiment can be successfully analysed if interactions are small enough to be ignored. Removing the interaction factor from the design then ‘frees up’ \((a-1)(b-1)\) degrees of freedom for estimating the residual variance. This strategy corresponds to merging the A:B interaction factor with experimental unit factor (E), resulting in the experimental structure in Figure 6.6(right). The resulting variance component for (E) then entails the former residual variance and the (negligible) variance from the interactions.

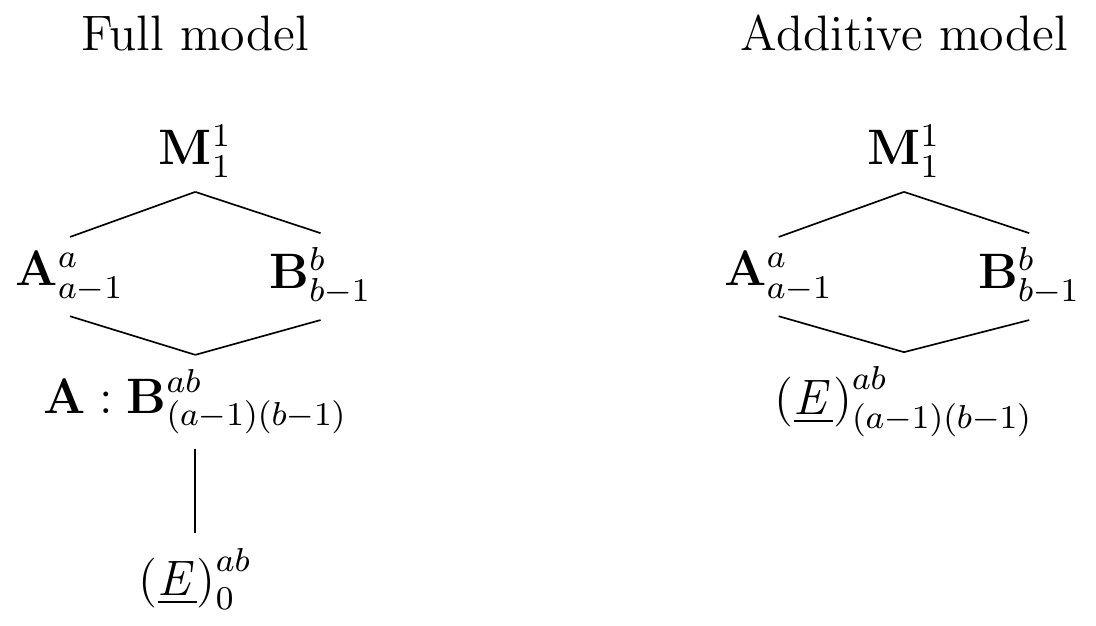
Figure 6.6: Left: experiment structure for \(a\times b\) two-way factorial with single observation per cell; no residual degrees of freedom left. Right: same experiment based on additive model removes interaction factor and frees degrees of freedom for estimating residual variance.

The crucial assumption of no interaction is sometimes justified on subject-matter grounds or from previous experience. If a non-replicated factorial design is run without a clear justification, we can use an ingenious procedure by Tukey to test for an interaction (J. W. Tukey 1949). It applies if at least one of the two treatment factors has three levels or more. Instead of the full model with interaction, Tukey proposed to use a more restricted version of the interaction: a multiple of the product of the two main effects. The corresponding model is \[ y_{ij} = \mu + \alpha_i + \beta_j + \lambda\cdot\alpha_i\cdot\beta_j + e_{ij}\;, \] where \(\lambda\) is an unknown parameter. We test the hypothesis \(H_0: \lambda=0\) of no interaction using one degree of freedom from the residuals by calculating the ‘interaction’ degrees of freedom \[ \text{SS}_\lambda = \frac{\left(\sum_{i=1}^a\sum_{j=1}^b y_{ij}\cdot(\bar{y}_{i\cdot}-\bar{y}_{\cdot\cdot})\cdot(\bar{y}_{\cdot j}-\bar{y}_{\cdot\cdot})\right)^2} {\left(\sum_{i=1}^a(\bar{y}_{i\cdot}-\bar{y}_{\cdot\cdot})^2\right)\cdot\left(\sum_{j=1}^b(\bar{y}_{\cdot j}-\bar{y}_{\cdot\cdot})^2\right)}\;. \] If \(H_0\) is true, then the test statistic \[ F = \frac{\text{SS}_\lambda /1 }{\text{MS}_\text{res}} \sim F_{1,ab-(a+b)} \] has an \(F\)-distribution with one numerator and \(ab-(a+b)\) denominator degrees of freedom. This procedure is implemented in the functions tukey.1df() from package dae and tukey.test() from package additivityTests (Rusch et al. 2009).

For our drug-diet with only a single observation per treatment group, this test has only one numerator and one denominator degree of freedom, and consequently very low power. We find a \(p\)-value of 0.99.

6.4.3 Higher-order factorials

We can construct factorial designs for any number of factors with any number of levels, but there is often a limit beyond which they become hard to implement and more difficult to interpret. For one, the number of combinations increases exponentially with the number of factors, and the more levels we consider per factor, the more combinations we get. For example, introducing the vendor as a third factor with two levels into our drug-diet example already yields \(3\cdot 2\cdot 2=12\) combinations, and introducing a fourth three-level factor increases this number further to \(12\cdot 3=36\) combinations. In addition, these two extensions yield additional interactions between three and even four factors.

A three-way model

We illustrate higher-order factorials using a three-way factorial with three generic factors A with \(a\) levels, B (\(b\) levels), and C (\(c\) levels). The experiment design is shown in Figure 6.7 with \(n\) replicates per treatment and the corresponding linear model is \[ y_{ijkl} = \mu_{ijk} + e_{ijkl} = \mu + \alpha_i + \beta_j + \gamma_k + (\alpha\beta)_{ij} + (\alpha\gamma)_{ik} + (\beta\gamma)_{jk} + (\alpha\beta\gamma)_{ijk} + e_{ijkl}\;. \] Our model has three main effects, three two-way interactions and one three-way interaction. For example, with Sex as a third factor in our drug-diet example, a three-way interaction \((\alpha\beta\gamma)_{ijk}\) would arise if the drug-diet interaction that we observed for \(D2\) compared to placebo under both diets only occurs in female mice, but not in male mice (or with different magnitude). In other words, the two-way interaction itself depends on the level of the third factor and we are now dealing with a difference of a difference of differences.

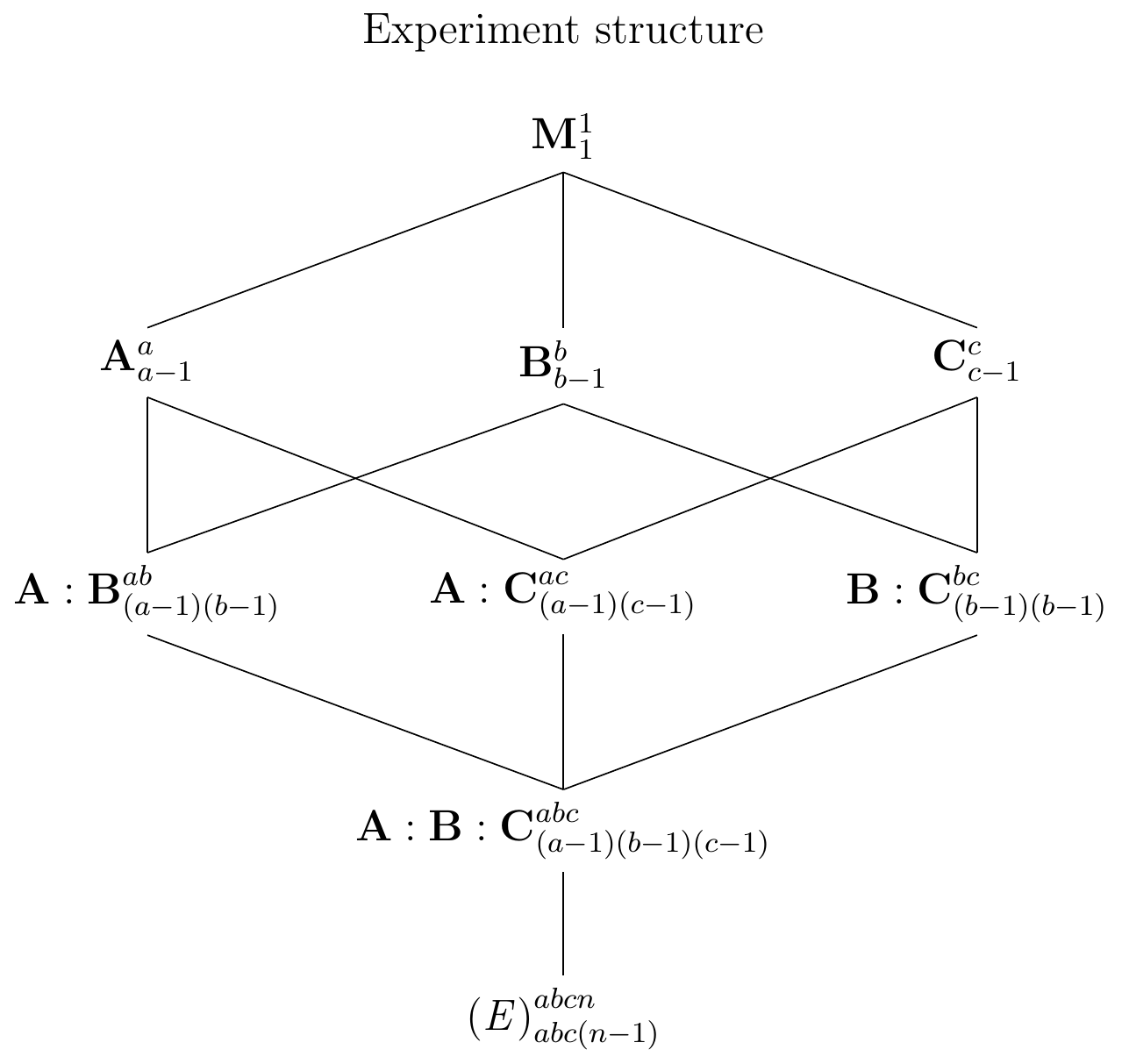
Figure 6.7: Generic three-way factorial design with completely randomized treatment allocation. The factorial contains three two-way and one three-way interaction.

An additional example of a three-way analysis of variance from ‘real life’ is the following: a study concerned the inflammation reaction in mice and potential drug targets to suppress inflammation. It was already known that a particular pathway gets activated to trigger inflammation response, and one protein in that pathway is a known drug target. In addition, there was preliminary evidence that inflammation sometimes triggers even if the pathway is knocked out. A \(2\times 2\times 2=2^3\)-factorial experiment was conducted with three treatment factors: (i) genotype: wildtype mice / knock-out mice without the known pathway; (ii) drug: placebo treatment / known drug; (iii) waiting time: 5 hours / 8 hours between inducing inflammation and administering the drug or placebo. Several mice were used for each of the 8 combinations and their protein levels measured using mass spectrometry. The main focus of inference is the genotype-by-drug interaction, which would indicate if an alternate activation exists and how strong it is. The three-way interaction then provides additional information about difference in activation times between the known and a potential unknown pathway.

Strategies for high-order factorials

The implementation and analysis of factorial designs becomes more challenging as the number of factors and their levels increases. First, the number of parameters and degrees of freedom increase rapidly with the order of the interaction. For example, if three treatment factors are considered with three levels each, then \(a=b=c=3\), yielding one grand mean parameter, \(a-1=b-1=c-1=2\) main effect parameters per factor (6 in total), \((a-1)(b-1)=4\) two-way interaction parameters per interaction (12 in total), and \((a-1)(b-1)(c-1)=8\) parameters for the three-way interaction, with a total of \(1+6+12+8=27\) parameters to describe the full model. Of course, this number is identical to the number \(3^3=27\) of possible treatment combinations (the model is saturated) and the experiment already requires 54 experimental units for \(n=2\) replicates.

In addition, the interpretation of an interaction becomes more intricate the higher its order: already a three-way interaction describes a difference of a difference of differences. In practice, interactions of order higher than three are rarely considered in a final model due to difficulties in interpretation, and already three-way interactions are not very common.

If higher-order interactions do occur, are significant and of considerable size, one strategy for simplifying the analysis is to stratify the analysis altogether by one of the factors. For example, with a significant and large three-way interaction, we could stratify by sex and produce two separate models, one for male and one for female mice, studying the effect of drug and diet independently for both sexes. The advantage of this approach is the easier interpretation, but we are also effectively halving the experiment size, such that information on drug and diet gained from one sex does not transfer easily into information for the other sex. In addition, interaction effects involving the sex factor cannot be studied if this factor was used for stratification of the experiment, but the effects for each level of stratification can be given independently.

With more than three factors, even higher-order interactions can be considered. Statistical folklore and practical experience suggest that interactions often become less pronounced the higher their order. Thus, if there are no substantial two-way interactions, then there is usually no reason to look into interactions of order three or higher.

If we have several replicate observations per treatment, then we can estimate the full model with all interactions, and use the marginality principle to reduce the model by removing higher-order interactions that are small and non-significant. If only one observation per treatment group ios available, a reasonable strategy is to exclude the highest-order interaction term to free its degrees of freedom for variance estimation. Since this interaction has typically many degrees of freedom, we can then continue with model reduction based on the \(F\)-tests.

There are two more strategies that are commonly used and very powerful when applicable. Screening experiments often involve a large number of factors, but the inference focuses on finding a subset of factors that is relevant for further investigation. Here, one often concentrates on main effects only to determine the relevant factors for further experimentation. The use of fractional factorial designs can substantially reduce the experiment size by deliberately confounding some effects; we discuss these two strategies in detail in Chapter 9.

6.5 Contrast analysis

Linear contrasts allow a more targeted analysis of treatment effects just like in the one-way ANOVA. Contrasts are sometimes defined using the parameters of the parametric model, but a conceptually simpler approach is to define them directly on the treatment group means \(\mu_{ij}\). In R, we can use the emmeans() and contrast() functions. For our drug-diet example, the following code estimates the ANOVA model and calculates the group means:

m = aov(y~drug*diet, data=d)
em = emmeans(m, ~drug+diet)

Table 6.3: Estimated cell means for three drugs and two diets.

Drug	Diet	Mean	se	df	LCL	UCL
Placebo	low fat	9.18	0.59	18	7.93	10.42
D1	low fat	14.17	0.59	18	12.93	15.42
D2	low fat	12.63	0.59	18	11.38	13.87
Placebo	high fat	10.65	0.59	18	9.41	11.90
D1	high fat	14.56	0.59	18	13.31	15.81
D2	high fat	9.83	0.59	18	8.58	11.07

The six group means are shown in Table 6.3; the formulae ~drug+diet sorts the means first by diet level, and then by drug level, while the alternative ~diet+drug would sort first by drug level and then by diet level.

6.5.1 Comparing each drug between diets

The \(F\)-test for the interaction factor indicates that the diet affects the drugs differently, and we ask how each drug compares between the diets on first set of contrasts \[ \Psi(\mathbf{w}_1) = \mu_{11} - \mu_{12}\,,\quad \Psi(\mathbf{w}_2) = \mu_{21} - \mu_{22}\,,\quad\text{and}\quad \Psi(\mathbf{w}_3) = \mu_{31} - \mu_{32}\;, \] where \(\mathbf{w}_1=(1,0,0,-1,0,0)\) is the weight vector for comparing the placebo effect between low fat and high fat, and \(\mathbf{w}_2=(0,1,0,0,-1,0)\) and \(\mathbf{w}_3=(0,0,1,0,0,-1)\) are the weight vectors for \(D1\) and \(D2\).

We estimate the contrasts using R as before: we estimate the ANOVA model using aov() and the group means via emmeans(). We then specify our contrasts as a named list psi and estimate them with contrast():

# Fit linear model
m = aov(y~drug*diet, data=d)
# Estimate cell means for drug x diet table
em = emmeans(m, ~drug+diet)
# Define list of contrast weight vectors
psi = list("Placebo low - Placebo high"=c(1,0,0,-1,0,0),
           "D1 low - D1 high"=c(0,1,0,0,-1,0),
           "D2 low - D2 high"=c(0,0,1,0,0,-1))
# Compute contrast estimates and unadjusted tests
ct = contrast(em, psi, adjust="none")
# Compute contrast estimates and unadjusted confidence intervals
ci = confint(ct)

Table 6.4: Contrast estimates and 95%-confidence intervals for comparing individual drugs under low and high fat diet

contrast	estimate	SE	df	lower.CL	upper.CL
Placebo low - Placebo high	-1.48	0.84	18	-3.24	0.29
D1 low - D1 high	-0.39	0.84	18	-2.15	1.37
D2 low - D2 high	2.80	0.84	18	1.04	4.57

The results in Table 6.4 give quantitative confirmation of our earlier suspicion: both placebo and \(D1\) show lower responses under the low fat diet compared to high fat, but the resulting difference is explainable by sampling variation and cannot be distinguished from zero with the given data. In contrast, the response for \(D2\) is substantially and significantly higher under a low fat compared to a high fat diet. Confidence intervals are fairly wide due to the small sample size, and the experiment is likely underpowered.

Note that in each case, the contrast’s standard error is based on 18 degrees of freedom, the degrees of freedom for the residual variance. Even though the first contrast, for example, only looks at data from two out of six cells, the degrees of freedom and the residual variance estimate are based on all data. We also note that the three contrasts are orthogonal, and we do not require a multiple testing procedure. Since we have six cell means, we can find five orthogonal contrasts, and our current set does not fully exhaust the information in the dataset.

6.5.2 Interaction contrasts: comparing drugs to placebo between diets

The previous contrasts looked at the difference in enzyme levels between diets for each drug. If such a difference exists for the placebo treatment, however, the interpretation of a difference in \(D1\) or \(D2\) requires more consideration. Since the placebo treatment provides the control group for each diet, we should compare differences for each drug to the difference in placebo to estimate the portion of the enzyme level differene that is due to the drug and not due to the diet.

For \(D1\), for example, we can calculate the difference in enzyme levels under each diet to the placebo value, and then determine the difference between these two effects. The corresponding contrast is \[ \Psi(\mathbf{w}_8) = (\mu_{21}-\mu_{11}) - (\mu_{22}-\mu_{12})\;. \] Equivalently, we can compare the difference between the two diets under \(D1\) to the difference under placebo. This give the same contrast, with terms sorted differently: \[ \Psi(\mathbf{w}_8) = (\mu_{21}-\mu_{22}) - (\mu_{11}-\mu_{12})\;. \] The corresponding contrast for \(D2\) is \[ \Psi(\mathbf{w}_9) = (\mu_{31}-\mu_{32}) - (\mu_{11}-\mu_{12})\;. \]

Table 6.5: Interaction contrast estimates and Bonferroni-adjusted 95%-confidence intervals.

Contrast	Estimate	LCL	UCL
(D1 low - D1 high) - (Pl. low - Pl. high)	1.09	-1.81	3.99
(D2 low - D2 high) - (Pl. low - Pl. high)	4.28	1.38	7.18

The estimates and 95%-confidence intervals are shown in Table 6.5. Not unexpected, we find that the change in response for \(D1\) is larger than the change in the control group, but not significantly so. We already know that \(D1\) enzyme levels are higher for both diets from the main effect contrasts, so this new result means that the difference between placebo and \(D1\) is identical for both diets. In other words, the response to \(D1\) changes from low fat to high fat by the same amount as the response to placebo. The two lines in Figure 6.1(B) should then be roughly parallel (not considering sample variation), as indeed they are.

In contrast, the change for \(D2\) is substantially and significantly larger than that for the control group. This is also in accordance with Figure 6.1(B): while the response to placebo is increasing slightly from low fat to high fat, the response to \(D2\) does the opposite and decreases substantially from low fat to high fat. This is reflected by the significant large positive contrast, which indicates that the change in \(D2\) between the two diets follows another pattern than the change in placebo, and goes in the opposite direction (placebo increases while \(D2\) decreases).

These contrasts are interaction contrasts, since they consider differences of differences; logically, they belong to the Drug:Diet interaction factor, and from the degrees of freedom in the Hasse diagram, we know that two orthogonal contrasts partition its sum of squares into two individual contributions. Our two interaction contrasts are not orthogonal and therefore do not partition the interaction sums of squares. An alternative set of two orthogonal interaction contrasts is shown in Table 6.6 and uses weight vectors \(\mathbf{w}_{10}=(0,-1,1,0,1,-1)\) and \(\mathbf{w}_{11}=(1,-1/2,1/2,-1,-1/2,+1/2)\). The first contrasts the effects of the two active drugs under the two diets, while the second compares the placebo treatment to the average of the two active drugs.

Table 6.6: Orthogonal contrast estimates and Bonferroni-adjusted 95%-confidence intervals.

Contrast	Estimate	LCL	UCL
(D1 low - D1 high) - (D2 low - D2 high)	3.19	0.29	6.09
(Pl. low - Pl. high) - avg(drug low - drug high)	-4.62	-7.13	-2.10

The results show that the difference in enzyme levels between the two diets is much larger for \(D1\) than for \(D2\), and much lower for placebo compared to the average of the two drugs. In how far the latter contrast is biologically meaningful is of course another question and our first set of non-orthogonal contrasts is likely more meaningful and easier to interpret.

6.6 Power analysis and sample size

The power analysis and determination of sample sizes for omnibus \(F\)-tests in a multi-way ANOVA follow the same principles as for a one-way ANOVA and are based on the noncentral \(F\)-distribution. Similarly, power analysis for linear contrasts is identical to the one-way ANOVA case, and the ideas of portable power can also be applied, so we give only brief additional remarks.

6.6.1 Main effects

To determine the power of an omnibus \(F\)-test for a main effect A, we need the significance level \(\alpha\), the effect size (\(f^2_\text{A}\) or \(\eta^2_\text{p, A}\)), and the residual variance \(\sigma_e^2\). The sample size \(n_A\) is now the number of samples per level of A, and is distributed evenly over the levels of all other factors crossed with A. For our generic two-way design with factors A and B with \(a\) and \(b\) levels, respectively, the number of samples per treatment combination is then \(n=n_A/b\). The degrees of freedom for the denominator are \(\text{df}_\text{res}=ab(n-1)\) for the full model with interaction, and \(\text{df}_\text{res}=nab-a-b+1\) for the additive model; we directly find them from the experiment diagram.

For our drug-diet example, we consider \(n_B=12\) mice per diet and thus \(n=12/3=4\) mice per drug-diet combination, a significance level of \(\alpha=5\%\) and use our previous estimate for the residual variance \(\hat{\sigma}_e^2=\) 1.5. These parameters provide a power of \(-\beta=\) 0.64 for detecting a minimal effect size of \(d_0=1\) or equivalently \(f^2_0=d_0^2/4=1/4\).

As a second example, we consider a ‘medium’ standardized main drug effect of \(f^2_0=0.25^2=0.0625\) and a desired power of 80% at a 5% significance level. This requires a sample size of \(n_A=\) 53 mice per drug level, about \(n=\) 27 mice per drug-diet treatment combination. The standardized difference between two drug averages is then \(d_0=\sqrt{f^2\cdot 6}=\) 0.61, corresponding to a raw difference in enzyme levels of \(\delta_0=d_0\cdot\sigma_e=\) 0.75 for the assumed residual variance.

Extending these ideas to main effects of higher-order factorial designs is straightforward and only requires that we correctly calculate the residual degrees of freedom to take account of the other factors in the design. The resulting sample size is then again per level of the factor of interest, and has to be divided by the product of the number of levels of all other factors to get to the sample size per treatment. For example, with a three-way design with \(a=b=4\) and \(c=5\) factor levels, a resulting sample size of \(n_A=60\) for an A main effect means that we need \(n=n_A/bc=3\) samples per treatment combination.

6.6.2 Interactions

We calculate the power for an interaction factor \(F\)-test using the same method as for a main effect. The denominator degrees of freedom are still the residual degrees of freedom, and we find the correct numerator degrees of freedom from the Hasse diagram. For our generic two-way example, these are \(ab(n-1)\) and \((a-1)(b-1)\), respectively, and the resulting sample size corresponds to \(n\) directly. For higher-order factorial designs, we again have to divide the resulting sample size by the product of levels of the factors not involved in the interaction.

The standardized effect size for an interaction A:B is \(f^2=\sum_i\sum_j(\alpha\beta)_{ij}/ab\sigma^2\), but defining a minimal effect size that corresponds to a biologically meaningful interaction can be challenging. Three options are (i) to define the interaction parameters \((\alpha\beta)_{ij}\) directly; (ii) define the expected responses \(\mu_{ij}\) for each combination of levels of A and B and work out the parameters from there; and (iii) use information about main effects from previous single-factor studies and define a level of attenuation of these effects due to the second factor.

We look into the third option more closely and denote the two main effect sizes of previous single-factor studies by \(f^2_\text{A, single}\) and \(f^2_\text{B, single}\); note that the main effects will likely change in a two-way design. The same situation occurs if we have reasonable guesses for the two isolated main effect sizes. We can then argue about how much attenuation or increase in the difference in response we expect for A, say, when looking at the low level of B compared to its high level. The effect size of the interaction is then about the same size as the single main effects if we expect a complete effect reversal, such as shown in Figure 6.4 (D). We can then use \(f^2_\text{A, single}\) as a reasonable expected effect size for the interaction and base out power analysis on this number. If we expect full attenuation of the effect of one factor, such as shown in Figure 6.4 (C), then the interaction effect size is about one-half the original single main effect size. With lower attenuation, the interaction effect decreases accordingly. From these considerations, we can find some (very rough) indications for the required sample size for detecting an interaction effect: the total sample size is roughly the same as for the original main effect for a complete effect reversal. If we needed \(n\) samples for detecting a certain minimal A main effect with given power, then we need again \(n\) samples for each level of A, which means \(n/b\) samples per treatment. If we expect full attenuation, the total required sample size doubles, and for a 50% attenuation, we are already at four times the sample size that we would need to detect the single-factor main effect. The arguments become much more involved for interactions of factors with more than two levels.

We can alternatively forsake a power analysis for the interaction omnibus \(F\)-test, and instead specify (planned) interaction contrasts. The problem of power and sample size is then shifted to corresponding analyses for contrasts, whose minimal effect sizes are often easier to define.

6.6.3 Contrasts

Power analysis for contrasts is identical to the one-way design as discussed in Section 5.1.8. For a two-way design with \(a\) and \(b\) levels, we can find \(ab-1\) orthogonal contrasts, \(a-1\) for the first main effect, \(b-1\) for the second, and \((a-1)(b-1)\) to partition the interaction. A sensible strategy is to define the planned contrasts for the experiment, use power analysis to determine the required sample size for each contrast, and then use the largest resulting sample size when implementing the experiment.

If the contrasts are not orthogonal, we should consider adjustments for multiple testing. Since we do not have the resulting \(p\)-values yet, the Bonferroni correction is the only real choice for a set of general purpose contrasts. Thus, we perform the power analysis as usual, but use a significance level of \(\alpha/q\) for a set of \(q\) contrasts. The resulting required sample size is larger than for a single contrast.

6.6.4 Portable power

The portable power ideas translate directly from one-way ANOVA to multi-way ANOVA. For example, let us consider our three-way factorial design with treatment factors Drug, Diet, and Sex with \(a=3\), \(b=2\), and \(c=2\) levels, respectively, based on \(N=24\) mice with 2 mice per treatment. For a main effect omnibus-test for factor X, we use the relation \(\phi^2=f^2_\text{X}\cdot n_\text{X}\), where \(f^2_\text{X}\) is the standardized effect size for the factor main effect, and \(n_\text{X}\) is the sample size per level of X. Thus, the necessary sample size for detecting a medium drug main effect of at least \(f_\text{drug}=0.25\), using \(\phi\approx 2\), is \(n_\text{drug}=\) 64 mice per drug, and thus 16 mice per treatment for a significance level \(\alpha=5\%\) and 80% power.

A useful shortcut exists for the most frequent type of interaction contrast which uses two levels each of \(m\) treatment factors, with weights \(w_i=\pm 1\) for two chosen levels of each factor, and zero else, resulting in \(2^m\) non-zero entries in the weight vector \(\mathbf{w}\). The variance of such contrast is then \(\sigma_e^2/n\cdot 2^m\). For detecting a minimal contrast size of \(\Psi_0\) or a minimal distance \(\delta_0\) between any cell means in the contrast, the required sample size is \[ n = \frac{\phi^2}{\Psi_0^2/\sigma_e^2}\cdot 2^{m-3} \quad\text{respectively}\quad n = \frac{\phi^2}{\delta_0^2/\sigma_e^2}\cdot \frac{1}{2^{m-3}}\;. \] The sample size \(n\) is the number of samples for each combination of the treatment factors involved in the interaction.

References

Fisher, R. A. 1926. “The Arrangement of Field Experiments.” Journal of the Ministry of Agriculture of Great Britain 33: 503–13.

Nelder, J A. 1994. “The statistics of linear models: back to basics.” Statistics and Computing 4 (4). Kluwer Academic Publishers: 221–34. https://doi.org/10.1007/BF00156745.

Rusch, Thomas, Marie Šimečková, Karl Moder, Dieter Rasch, Petr Šimeček, and Klaus D. Kubinger. 2009. “Tests of additivity in mixed and fixed effect two-way ANOVA models with single sub-class numbers.” Statistical Papers 50 (4): 905–16. https://doi.org/10.1007/s00362-009-0254-4.

Tukey, J. W. 1949. “One Degree of Freedom for Non-Additivity.” Biometrics 5 (3): 232–42. http://www.jstor.org/stable/3001938.