Chapter 2 Review of Statistical Concepts

In this chapter, we briefly review some basic concepts in statistical inference for analyzing a given set of data. The material roughly covers a typical introductory course in statistics: describing variation, estimating parameters, and testing hypotheses in the context of normally distributed data. Throughout, we assume some prior exposure to the material at this level. The focus on the normal distribution avoids the need for more technically difficult mathematical and computational machinery and allows us to concentrate on the design rather than complex analysis aspects of an experiment in later chapters.

2.1 Probability

2.1.1 Random variables and distributions

Even under well controlled conditions, replicate measurements will deviate from each other to a certain degree. In biological experiments, for example, two main sources of this variation are heterogeneity of the experimental material and measurement uncertainties. After accounting for potential systematic differences, we can assign probabilities to these deviations.

A random variable maps a random event to a number, for example to a (random) deviation of an observed measurement from the underlying true value. We often denote a random variable by a capital letter and a specific observed realization or outcome by a the corresponding lower case letter. For example, we might be interested in the level of a specific liver enzyme in mouse serum. The data in Table 2.1 shows again the measured levels of ten randomly selected mice, where one sample was taken from each mouse, processed using a commercially available kit, and the enzyme level was quantified using a well-established assay.

Table 2.1: Measured enzyme levels of ten randomly selected mice.

1	2	3	4	5	6	7	8	9	10
8.96	8.95	11.37	12.63	11.38	8.36	6.87	12.35	10.32	11.99

We formally describe the observation for the \(i\)th mouse by the outcome \(y_i\) of its associated random variable \(Y_i\). The (probability) distribution of a random variable \(Y\) gives the probability of observing an outcome within a given interval. The probability density function (pdf) \(f_Y(y)\) and the cumulative distribution function (cdf) \(F_Y(y)\) of \(Y\) both describe its distribution. The area under the pdf between two values between \(a\) and \(b\) gives the probability that a realization of \(Y\) falls into the interval \([a,\,b]\) is given by the area under the pdf: \[ \mathbb{P}(Y\in [a,\,b]) = \mathbb{P}(a\leq Y\leq b) = \int_a^b f_Y(y')\,dy' = F_Y(b)-F_Y(a)\;, \] while the cdf gives the probability that \(Y\) will take any value lower or equal to \(y\): \[ F_Y(y) = \mathbb{P}(Y \leq y) = \int_{-\infty}^y f_Y(y') dy'\;. \] Often, it is reasonable to assume a normal (or Gaussian) distribution distribution for the data. This distribution has two parameters \(\mu\) and \(\sigma^2\) and its probability density function is \[ f_Y(y;\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}\cdot\exp\left(-\frac{1}{2}\cdot\left(\frac{y-\mu}{\sigma}\right)^2\right)\;, \] which yields the famous bell-shaped curve symmetric around a peak at \(\mu\) and with width determined by \(\sigma\). In our example, we have normally distributed observations with \(\mu=10\) and \(\sigma^2=2\), which yields the probability density function shown in Figure 2.1.

We write \(Y\sim N(\mu,\sigma^2)\) to say that the random variable \(Y\) has a normal distribution with parameters \(\mu\) and \(\sigma^2\). The density is symmetric around \(\mu\) and thus the probability that we observe an enzyme level lower than 10 is \(\mathbb{P}(Y\leq 10)=0.5\). The probability that the observed level falls above \(a=\) 12.7 is \(1-F_Y(y)=\int_{a}^\infty f_Y(y')dy'=0.975\) or 97.5%. More details on normal distributions and their properties are given in Section 2.1.6.

2.1.2 Quantiles

We often interested in the \(\alpha\)-quantile \(q_\alpha\) below which a realization falls with given probability \(\alpha\) such that \[ \mathbb{P}(Y\leq q_\alpha)=\alpha\;. \] The value \(q_\alpha\) depends on the distribution of \(Y\) and different distributions can have vastly different quantiles for the same \(\alpha\).

For our example, a new observation will be below the quantile \(q_{0.025}=\) 7.3 with probability \(2.5\%\) and below \(q_{0.975}=\) 12.7 with probability \(97.5\%\). These two quantiles are indicated by arrows in Figure 2.1 and each shaded area corresponds to a probability of \(2.5\%\).

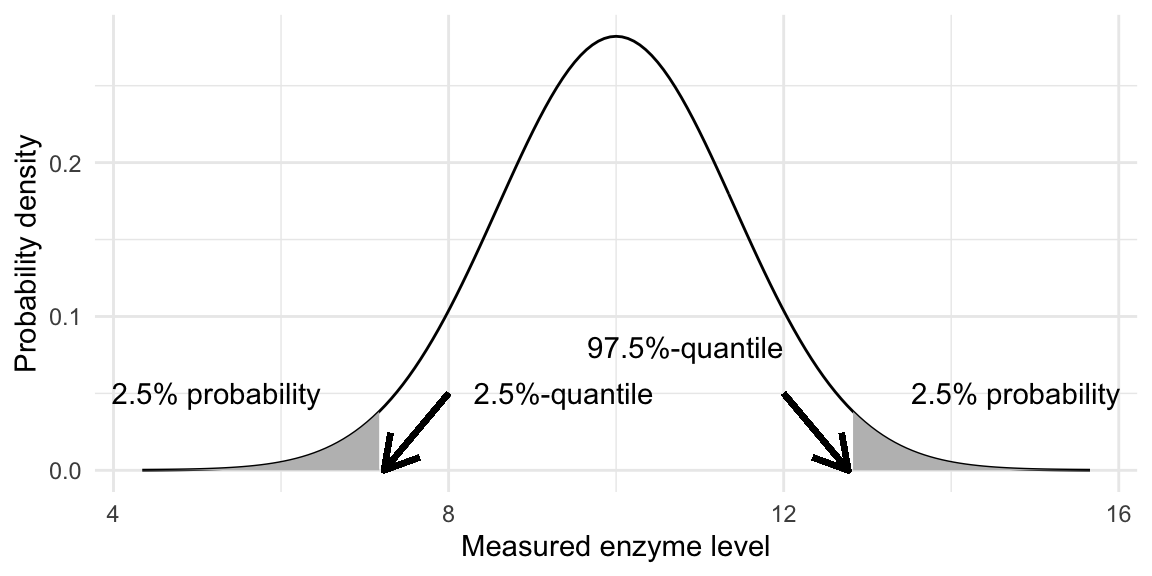
Figure 2.1: Normal density with 2.5% and 97.5-%-quantiles (arrows) and areas corresponding to 2.5-% probability under left and right tail (grey shaded areas).

2.1.3 Independence and conditional distributions

The joint distribution of two random variable \(X\) and \(Y\) is \(F_{X,Y}(x,y)=\mathbb{P}(X\leq x, Y\leq y)\), the probability that \(X\leq x\) and \(Y\leq y\) are simultaneously true. We can decompose this into a product of the marginal distribution \(\mathbb{P}(X\leq x)\) and the conditional distribution \(\mathbb{P}(Y\leq y | X\leq x)\) (read ``\(Y\) given \(X\)’’) that \(Y\) takes a value smaller or equal \(y\) if \(X\) takes a value lower or equal \(x\): \[ \mathbb{P}(X\leq x, Y\leq y) = \mathbb{P}(X\leq x)\cdot\mathbb{P}(Y\leq y | X\leq x) = \mathbb{P}(Y\leq y)\cdot\mathbb{P}(X\leq x | Y\leq y)\;. \]

In our example, the enzyme levels \(Y_i\) and \(Y_j\) of two different mice are independent: their realizations \(y_i\) and \(y_j\) are both from the same distribution, but knowing the measured level of one mouse will tell us nothing about the level of another mouse and \(\mathbb{P}(Y_i\leq y_i | Y_j\leq y_j)=\mathbb{P}(Y_i\leq y_i)\).

The joint probability of two independent variables is the product of the two individual probabilities. For example, the probability that both mice yields measurements below 10 is \(\mathbb{P}(Y_i\leq 10, Y_j\leq 10)=\mathbb{P}(Y_i\leq 10)\cdot\mathbb{P}(Y_j\leq 10)=0.5\cdot 0.5=0.25\).

As an example of two dependent random variables, we might take a second sample from each mouse and measure the enzyme level of this sample. The resulting data are shown in Table 2.2. We immediately observe that the first and second measurements are much more similar within the same mouse than between two different mice.

Table 2.2: Measured enzyme levels of 10 lab mice, each mouse measured twice.

1	2	3	4	5	6	7	8	9	10
8.96	8.95	11.37	12.63	11.38	8.36	6.87	12.35	10.32	11.99
8.82	9.13	11.37	12.50	11.75	8.65	7.63	12.72	10.51	11.80

We denote by \(Y_{i,1}\) and \(Y_{i,2}\) the two measurements of the \(i\)th mouse. Then, \(Y_{i,1}\) and \(Y_{j,1}\) are independent since they are measurements on two different mice and \(\mathbb{P}(Y_{i,1}\leq 10|Y_{j,1}\leq 10)=\mathbb{P}(Y_i\leq 10)=0.5\), for example. In contrast, \(Y_{i,1}\) and \(Y_{i,2}\) are not independent, because they are two measurements on the same mouse: knowing the result of the first measurements gives us a strong indication about the value of the second measurement and \(\mathbb{P}(Y_{i,2}\leq 10|Y_{i,1}\leq 10)\) is likely to be much higher than 0.5, because if the first sample yields a level below 10, the second will also tend to be below 10. We discuss this in more detail shortly when we look at covariances and correlations.

2.1.4 Expectation and variance

Instead of working with the full distribution of a random variable \(Y\), it is often sufficient to summarize its properties by the expectation and variance, which roughly speaking give the position around which the density function spreads, and the dispersion of values around this position, respectively.

The expected value (or expectation, sometimes also called mean or average) of a random variable \(Y\) is a measure of location. It is defined as the weighted average of all possible realizations \(y\) of \(Y\), taking the density \(f_Y(y)\) at each point as its weight: \[ \mathbb{E}(Y) = \int_{-\infty}^{+\infty} y'\cdot f_Y(y') dy'\;. \]

The expectation is linear and the following arithmetic rules apply for any two random variables \(X\) and \(Y\) and any non-random constant \(a\): \[\begin{equation*} \mathbb{E}(a) = a \,,\; \mathbb{E}(a+X) = a+\mathbb{E}(X) \,,\; \mathbb{E}(a\cdot X) = a\cdot\mathbb{E}(X)\,,\; \mathbb{E}(X+Y) = \mathbb{E}(X)+\mathbb{E}(Y)\;. \end{equation*}\] If \(X\) and \(Y\) are independent, then the expectation of their product is the product of the expectations: \[\begin{equation*} \mathbb{E}(X\cdot Y) = \mathbb{E}(X)\cdot \mathbb{E}(Y)\;, \end{equation*}\] but note that in general \(\mathbb{E}\left(X \,/\, Y\right) \not= \mathbb{E}(X) \,/\, \mathbb{E}(Y)\) even for independent variables.

The variance of a random variable \(Y\), often denoted by \(\sigma^2\), is defined as \[ \text{Var}(Y) = \mathbb{E}\left(\left(Y-\mathbb{E}(Y)\right)^2\right)=\mathbb{E}(Y^2)-\mathbb{E}(Y)^2\;, \] the expected distance of a value of \(Y\) from its expectation, where the distance is measured as the squared difference. It is a measure of dispersion, describing how wide values spread around their expected value.

For a non-random constant \(a\) and two random variables \(X\) and \(Y\), the following arithmetic rules apply for variances: \[\begin{equation*} \text{Var}(a) = 0\,,\;\text{Var}(a + Y) = \text{Var}(Y)\,,\;\text{Var}(a\cdot Y) = a^2\cdot\text{Var}(Y)\;. \end{equation*}\] If \(X\) and \(Y\) are independent, then \[\begin{equation*} \text{Var}(X+Y) = \text{Var}(X)+\text{Var}(Y)\;, \end{equation*}\] and we will discuss the dependent case shortly. Moreover, the variation in the difference of two independent random variables is larger than the individual variances since \[\begin{equation*} \text{Var}(X-Y) = \text{Var}(X+(-1)\cdot Y) = \text{Var}(X)+(-1)^2\cdot\text{Var}(Y) = \text{Var}(X)+\text{Var}(Y)\;. \end{equation*}\]

For a normally distributed random variable \(Y\sim N(\mu,\sigma^2)\), the expectation and variance completely specify the full distribution, since \(\mu=\mathbb{E}(Y)\) and \(\sigma^2=\text{Var}(Y)\). For our example distribution in Figure 2.1, for example, the expectation \(\mu=10\) provides the location of the maximum of the density, and the variance \(\sigma^2\) corresponds to the width of the density curve around this location. The relation between a distribution’s parameters and its expectation and variance is in general much less direct for other distributions.

Given the expectation and variance of a random variable \(Y\), we can define a new random variable \(Z\) with expectation zero and variance one by shifting and scaling: \[ Z=\frac{Y-\mathbb{E}(Y)}{\sqrt{\text{Var}(Y)}}\quad\text{ has }\quad \mathbb{E} (Z)=0 \text{ and } \text{Var}(Z)=1\;. \] If \(Y\) is normally distributed with parameters \(\mu\) and \(\sigma^2\), then \(Z=(Y-\mu)/\sigma\) is also normally distributed with parameters \(\mu=0\) and \(\sigma^2=1\). In general, however, the distribution of \(Z\) will be of a different kind than the distribution of \(Y\). For example, \(Y\) might be a concentration and take only positive values, but \(Z\) is centered around zero and will take positive and negative values.

The realizations of \(n\) independent and identically distributed random variables \(Y_i\) are often summarized by their arithmetic mean \(\bar{Y}=\frac{1}{n}\sum_{i=1}^n Y_i\). Since \(\bar{Y}\) is a function of random variables, it is itself a random variable and therefore has a distribution. Indeed, if the individual \(Y_i\) are normally distributed, then \(\bar{Y}\) also has a normal distribution. Assuming that all \(Y_i\) have expectation \(\mu\) and variance \(\sigma^2\), we can determine the expectation and variance of the arithmetic mean. First, we find that its expectation is identical to the expectation of the individual \(Y_i\): \[ \mathbb{E}(\bar{Y}) = \mathbb{E}\left(\frac{1}{n}\sum_{i=1}^n Y_i\right) = \frac{1}{n}\sum_{i=1}^n \mathbb{E}(Y_i) = \frac{1}{n}\sum_{i=1}^n \mu = \mu\;. \] However, its variance is smaller than the individual variances, and decreases with the number of random variables: \[ \text{Var}(\bar{Y}) = \text{Var}\left(\frac{1}{n}\sum_{i=1}^n Y_i\right) = \frac{1}{n^2}\sum_{i=1}^n\text{Var}(Y_i) = \frac{1}{n^2}\cdot n\cdot \sigma^2 = \frac{\sigma^2}{n}\;. \] For our example, the average of the ten measurements of enzyme levels has expectation \(\mathbb{E}(\bar{Y})=\mathbb{E}(Y_i)=10\), but the variance \(\text{Var}(\bar{Y})=\sigma^2/10=\) 0.2 is only one-tenth of the individual variances \(\text{Var}(Y_i)=\sigma^2=\) 2. The average of ten measurements therefore shows less dispersion around the mean than each individual measurement. Since the sum of normally distributed random variables is again normally distributed, we thus know that \(\bar{Y}\sim N(\mu, \sigma^2/n)\) with \(n=10\) for our example.

While the variance of a sum is the sum of the variances, the variance does not behave nicely to changes in the measurement scale: if \(Y\) is measured in meters, the variance is given in square-meters, and a shift to centimeters multiplies the measurements by 100, but the variances by \(100^2=10\,000\). We therefore often describe the scale of the distribution by the standard deviation \[ \text{sd}(Y)=\sqrt{\text{Var}(Y)}\;. \] It is a measure of dispersion in the same physical units as the random variable that behaves nicely to changes in scale, but is no longer additive: \[\begin{equation*} \text{sd}(a\cdot Y) = |a|\cdot\text{sd}(Y) \quad\text{but}\quad \text{sd}(X\pm Y) = \sqrt{\text{sd}(X)^2+\text{sd}(Y)^2} \text{ for independent $X,Y$}\;. \end{equation*}\] For our example, we find \(\text{sd}(Y_i)=\) 1.41 and \(\text{sd}(\bar{Y}_i)=\) 0.45.

2.1.5 Covariance and correlation

The idea of the variance as describing dispersion extends to the joint distribution of two random variables \(X\) and \(Y\) via the covariance \[ \text{Cov}(X,Y) = \mathbb{E}\left((X-\mathbb{E}(X))\cdot(Y-\mathbb{E}(Y))\right)\;, \] which measures the dependency between \(X\) and \(Y\): the covariance is large and positive if a large deviation of \(X\) from its expectation is associated with a large deviation of \(Y\) in the same direction; it is large and negative if these directions are reverse; the covariance is small when deviations of \(X\) and \(Y\) from their respective expectations are independent.

The covariance of a random variable with itself is its variance \(\text{Cov}(X,X)=\text{Var}(X)\) and the covariance is zero if \(X\) and \(Y\) are independent (the converse is not true!). The covariance is linear in both arguments, in particular: \[\begin{equation*} \text{Cov}(a\cdot X+b\cdot Y, Z) = a\cdot\text{Cov}(X,Z)+b\cdot\text{Cov}(Y,Z)\;, \end{equation*}\] and similar for the second argument. A related measure is the correlation \[ \text{Corr}(X,Y) = \frac{\text{Cov}(X,Y)}{\text{sd}(X)\cdot\text{sd}(Y)}\;, \] often denoted by the greek letter \(\rho\). In contrast to the covariance, which can take any positive or negative value and whose physical unit is the product of the units of \(X\) and \(Y\), the correlation is a unit-less number between \(-1\) and \(+1\). Somewhat oversimplifying, \(-1\) means that \(Y\) goes down in the same manner as \(X\) goes up, and \(+1\) means both go up simultaneously in the same way, they are ``perfectly correlated’’.

The covariance is the missing ingredient to extend our formulas for the expectation and variance to the case of two dependent variables by \[ \mathbb{E}(X\cdot Y) = \mathbb{E}(X)\cdot\mathbb{E}(Y)+\text{Cov}(X,Y) \] and \[\begin{align*} \text{Var}(X+Y) &= \text{Var}(X) + \text{Var}(Y) + 2\cdot \text{Cov}(X,Y) \\ \text{Var}(X-Y) &= \text{Var}(X) + \text{Var}(Y) - 2\cdot \text{Cov}(X,Y)\;, \end{align*}\] which both reduce to the previous formulas if the variables are independent and \(\text{Cov}(X,Y)=0\).

In our first example, the measurements of enzyme levels in ten mice are independent. Therefore, \(\text{Cov}(Y_i,Y_i)=\text{Var}(Y_i)\) and for two different mice \(i\) and \(j\), \(\text{Cov}(Y_i,Y_j)=0\).

In our second example, two samples were measured for each of ten mice. We can write the random variable \(Y_{i,j}\) for the \(j\)th measurement of the \(i\)th mouse as the sum of a random variable \(M_i\) capturing the difference of the true enzyme level of mouse \(i\) to the expectation \(\mu=10\), and a random variable \(S_{i,j}\) capturing the difference between the observed enzyme level \(Y_{i,j}\) and the true level \(\mu+M_i\) for this mouse. Then, \[ Y_{i,j} = \mu + M_i + S_{i,j}\;, \] where \(\mu=10\), \(M_i\sim N(0,\sigma_m^2)\) and \(S_{i,j}\sim N(0,\sigma_e^2)\). If \(M_i\) and \(S_{i,j}\) are all independent, then the overall variance \(\sigma^2\) is decomposed into the two variance components: \(\sigma^2=\sigma_m^2+\sigma_e^2\).

If we plot the two measurements \(Y_{i,1}\) and \(Y_{i,2}\) of each mouse in a scatter-plot as in Figure 2.2A, we notice the high correlation: whenever the first measurement is high, the second measurement is also high. The covariance between these variables is \[\begin{align*} \text{Cov}(Y_{i,1}\,,Y_{i,2}) &= \text{Cov}(\mu+M_i+S_{i,1}\,,\mu+M_i+S_{i,2}) = \text{Cov}(M_i+S_{i,1}\,,M_i+S_{i,2}) \\ & = \underbrace{\text{Cov}(M_i\,,M_i)}_{\text{Var}(M_i)} + \underbrace{\text{Cov}(M_{i}\,,S_{i,2})}_{0} + \underbrace{\text{Cov}(S_{i,1}\,,M_{i})}_{0} + \underbrace{\text{Cov}(S_{i,1}\,,S_{i,2})}_{0} \\ & = \sigma_m^2\;, \end{align*}\] and the correlation is \[\begin{equation*} \text{Corr}(Y_{i,1},Y_{i,2}) = \frac{\text{Cov}(Y_{i,1},Y_{i,2})}{\text{sd}(Y_{i,1})\cdot\text{sd}(Y_{i,2})} = \frac{\sigma_m^2}{\sigma_m^2+\sigma_s^2}\;. \end{equation*}\] With \(\sigma_m^2=\) 1.9 and \(\sigma_e^2=\) 0.1, the correlation is extremely high at 0.95. This can also be seen in Figure 2.2B, which shows the two measurements for each mouse separately. Here, the magnitude of the differences between the individual mice (grey points) is related to \(\sigma_m^2\), while the magnitude of differences between the two measurements of any mouse (plus and cross) is much smaller and is related to \(\sigma_e^2\).

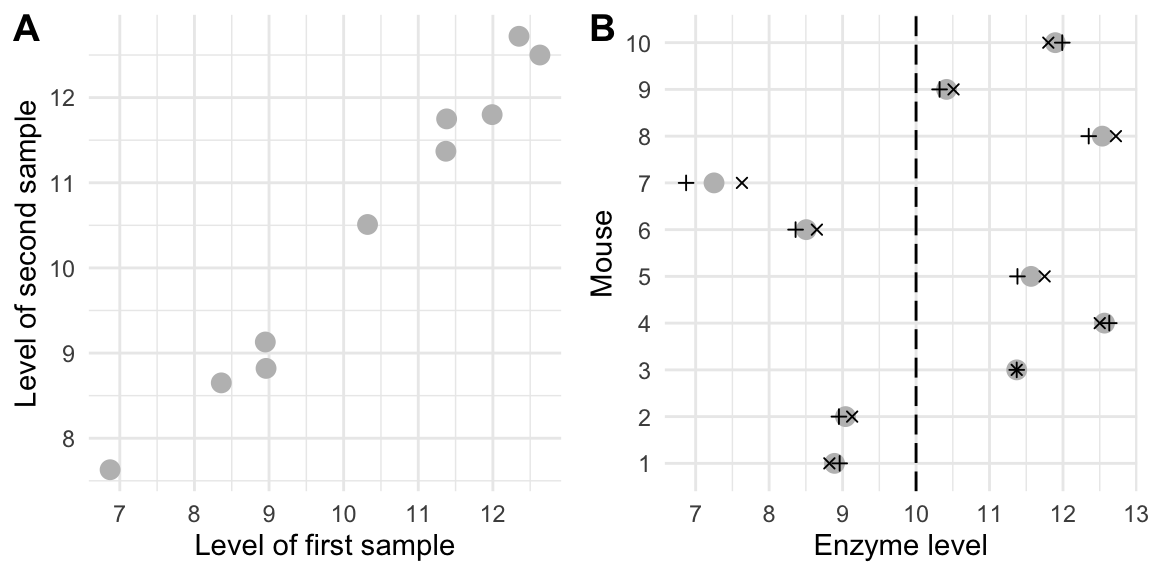
Figure 2.2: (A) Scatterplot of the enzyme levels of the first and second sample for each mouse. The points lie close to a line, indicating a very high correlation between the two samples. (B) Average (grey) and first (plus) and second (cross) sample enzyme level for each mouse. The dashed line is the average level in the mouse population.

As a third example, we consider the arithmetic mean of independent random variables and determine the covariance \(\text{Cov}(Y_i,\bar{Y})\). Because \(\bar{Y}\) is computed using \(Y_i\), these two random variables cannot be independent and we expect a non-zero covariance. Using the linearity of the covariance we get: \[\begin{equation*} \text{Cov}(Y_i,\bar{Y}) = \text{Cov}\left(Y_i,\frac{1}{n}\sum_{j=1}^n Y_j\right) = \frac{1}{n}\sum_{j=1}^n \text{Cov}(Y_i,Y_j) = \frac{1}{n}\cdot \text{Cov}(Y_i,Y_i) = \frac{\sigma^2}{n}\;, \end{equation*}\] using the fact that \(\text{Cov}(Y_i,Y_j)=0\) for \(i\not=j\). Thus, the covariance decreases with increasing number of random variables, because the variation of the average \(\bar{Y}\) depends less and less on each single variable \(Y_i\).

2.1.6 Common distributions

We encounter four families of distributions in the next chapters, and briefly gather some of their properties here for future reference. We assume that all data follow some normal distribution describing the errors due to sampling and measurement, for example. Derived from that are (i) the \(\chi^2\)-distribution related to estimates of variance, (ii) the \(F\)-distribution related to the ratio of two variance estimates, and (iii) the \(t\)-distribution related to estimates of means and differences in means.

Normal distribution

The normal distribution is well-known for its bell-shaped density, shown in Figure 2.3A for three combinations of its two parameters \(\mu\) and \(\sigma^2\). The special case of \(\mu=0\) and \(\sigma^2=1\) is called the standard normal distribution.

The omnipresence of the normal distribution can be partly explained by the central limit theorem, which states that if we have a sequence of random variables with identical distribution (for example, describing the outcome of many measurements), then the sum of these, properly scaled, will have a normal distribution, no matter what distribution each single random variable has. Technically, if \(Y_1,\dots,Y_n\) are independent and identically distributed with mean \(\mathbb{E}(Y_i)=\mu\) and variance \(\text{Var}(Y_i)=\sigma^2\), then the arithmetic mean \(S_n=(Y_1+\cdots +Y_n)/n\) approaches a normal distribution as \(n\) increases: \[ \sqrt{n}\cdot\left(S_n-\mu\right) \sim N(0,\sigma^2)\text{ as $n\to\infty$.} \]

If \(X\sim N(\mu_X,\sigma^2_X)\) and \(Y\sim N(\mu_Y,\sigma^2_Y)\) are two normally distributed random variables, then their sum \(X+Y\) is also normally distributed with parameters \[ \mathbb{E}(X+Y)=\mu_X+\mu_Y,\; \text{Var}(X+Y)=\sigma^2_X+\sigma^2_Y+2\cdot\text{Cov}(X,Y)\;. \]

Any normally distributed variable \(Y\sim N(\mu,\sigma^2)\) can be transformed into a standard normal variable by subtracting the mean and dividing by the standard deviation: \(Z=\frac{Y-\mu}{\sigma}\sim N(0,1)\). The \(\alpha\)-quantile of the standard normal distribution is denoted by \(z_\alpha\).

A few properties of the normal distribution are good to remember. If \(Y\sim N(\mu,\sigma^2)\), then the probability that \(Y\) will fall into an interval \(\mu\pm\sigma\) of one standard deviation around the mean is about 70%; for two standard deviations \(\mu\pm 2\sigma\), the probability is about 95%; and for three standard deviations, it is larger than 99%. In particular, the 2.5% and 97.5% quantiles of a standard normal distributions are \(z_{0.025}=-1.96\) and \(z_{0.975}=+1.96\) and can be conveniently taken to be \(\pm 2\) for approximate calculations.

\(\chi^2\) distribution

If \(Y_1,\dots,Y_n\sim N(0,1)\) are independent and standard normal, then the sum of their squares \[ \sum_{i=1}^n Y_i^2 \sim \chi^2_n \] has a \(\chi^2\) (read: ``chi-squared’’) distribution with \(n\) degrees of freedom. The distribution has expectation \(n\) and variance \(2n\), and the degrees of freedom \(n\) is its only parameter. It occurs when we are estimating the variance of a normally distributed random variable from a set of measurements, and is used to establish confidence intervals of variance estimates (Section 2.2.4.2). We denote by \(\chi^2_{\alpha,\,n}\) the \(\alpha\)-quantile on \(n\) degrees of freedom.

Its density for 3, 5, and 10 degrees of freedom is shown in Figure 2.3B. Note that the densities are asymmetric, only defined for non-negative values, and the maximum does not coincide with the expected value (for \(n=5\), the expected value is 5, but the maximum of the dotted curve is at around 3).

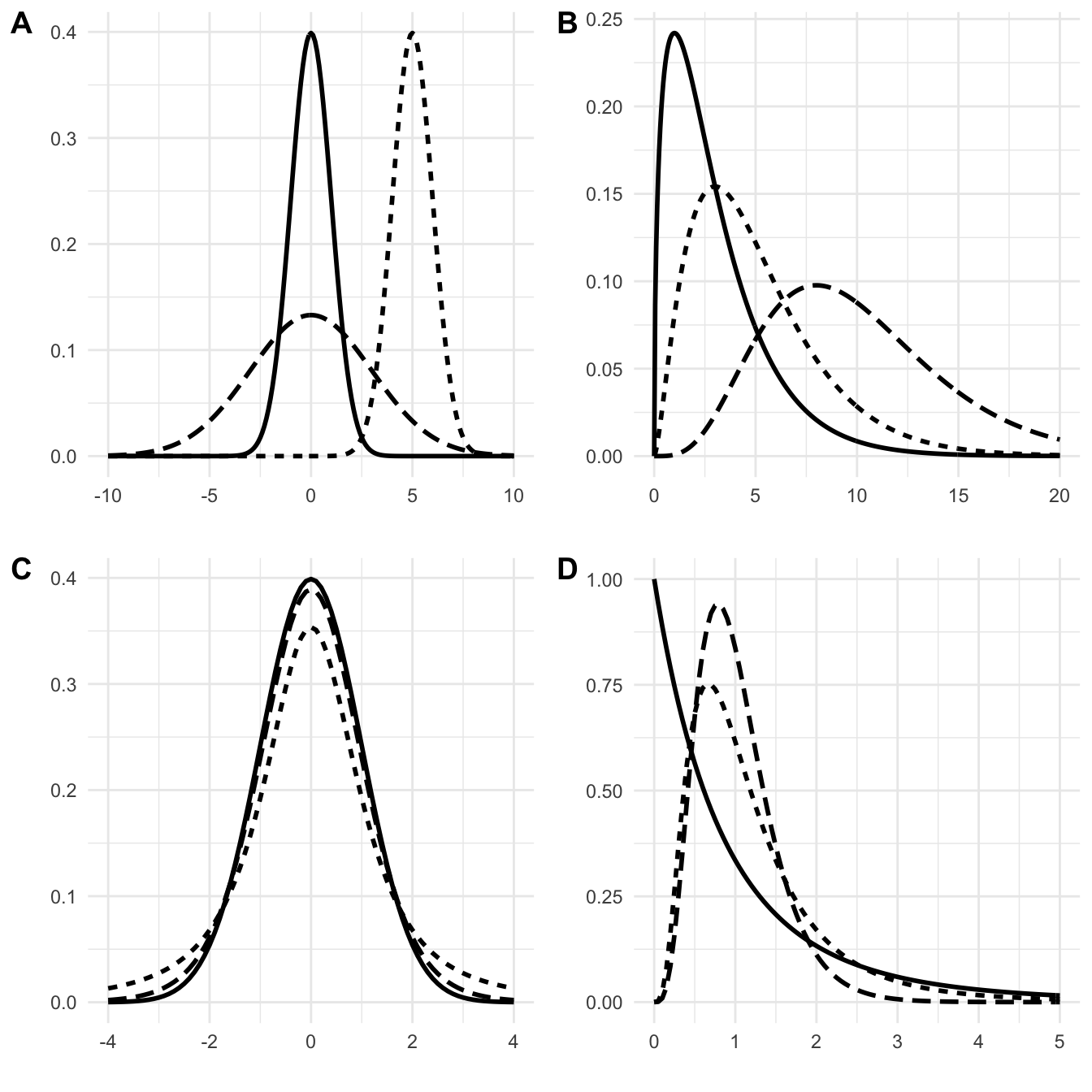
Figure 2.3: Probability densities of various distributions. A: normal distributions. Solid: standard normal with mean \(\mu=0\), standard deviation \(\sigma=1\); long-dashed (scaled): \(\mu=0\), \(\sigma=3\); dotted (shifted): \(\mu=5\), \(\sigma=1\). B: chi-square distributions with 3 (solid), 5 (dotted) and 10 (dashed) degrees of freedom. C: t-distributions with 2 (dotted) and 10 (dashed) degrees of freedom and standard normal density (solid). D: F-distributions with \((n=2, m=10)\) numerator/denominator degrees of freedom (solid), respectively \((n=10, m=10)\) (dotted) and \((n=10, m=100)\) (dashed).

The sum of two independent \(\chi^2\)-distributed random variables is again \(\chi^2\)-distributed, with degrees of freedom the sum of the two individual degrees of freedom: \[ X\sim\chi^2_n\text{ and }Y\sim\chi^2_m \implies X+Y\sim \chi^2_{n+m}\;. \] Moreover, if \(\bar{X}=\sum_{i=1}^n X_i/n\) is the average of \(n\) standard normally distributed variables, then \[ \sum_{i=1}^n (X_i-\bar{X})^2 \sim \chi^2_{n-1} \] also has a \(\chi^2\)-distribution, where one degree of freedom is ‘lost’ because we can calculate any summands from the remaining \(n-1\).

If the random variables \(Y_i\sim N(\mu_i,1)\) are normally distributed with unit variance but individual (potentially non-zero) means \(\mu_i\), then \(\sum_i Y_i^2\sim\chi^2(\lambda)\) has a noncentral \(\chi^2\)-distribution with noncentrality parameter \(\lambda=\sum_i\mu_i^2\). This distribution plays a role in sample size determination, for example.

t-distribution

If \(X\) has a standard normal distribution, and \(Y\) is independent of \(X\) and has a \(\chi^2_n\) distribution, then the random variable \[ \frac{X}{\sqrt{Y/n}} \sim t_n \] has a \(t\)-distribution with \(n\) degrees of freedom. This distribution has expectation zero and variance \(n/(n-2)\) and occurs frequently when studying the sampling distribution of normally distributed random variables whose expectation and variance are estimated from data. It most famously underlies the Student’s \(t\)-test, which we discuss in Section 2.3.1, and plays a prominent role in finding confidence intervals of estimates of averages (Section 2.2.4.1). The \(\alpha\)-quantile is denoted \(t_{\alpha,\,n}\).

The density of the \(t\)-distribution looks very similar to that of the standard normal distribution, but has ‘thicker tails’. As the degrees of freedom \(n\) get larger, the two distributions get more similar, and the \(t\)-distribution approaches the standard normal distribution in the limit: \(t_\infty= N(0,1)\). Two examples of \(t\)-distributions together with the standard normal distribution for comparison are shown in Figure 2.3C.

If the numerator \(X\sim N(\mu,1)\) has a non-zero expectation, then \(X/(\sqrt{Y/n})\sim t_n(\eta)\) has a noncentral \(t\)-distribution with noncentrality parameter \(\eta=\mu/(\sqrt{Y/n})\); this distribution is used in determining sample sizes for \(t\)-tests, for example.

F-distribution

If \(X\sim\chi^2_n\) and \(Y\sim\chi^2_m\) are two independent \(\chi^2\)-distributed random variables, then their ratio, scaled by the degrees of freedom, has an \(F\)-distribution with \(n\) numerator degrees of freedom and \(m\) denominator degrees of freedom, which are its two parameters: \[ \frac{X/n}{Y/m}\sim F_{n,m}\;. \] This distribution has expectation \(m/(m-2)\) and variance \(2m^2(n+m-2)/(n(m-2)^2(m-4))\). It occurs when investigating the ratio of two variance estimates and plays a central role in the analysis of variance, a key method in experimental design. The \(F\)-distribution is only defined for positive values and is asymmetric with a pronounced right tail (it has positive skew). Importantly, the sum of two \(F\)-distributed random variables does not have an \(F\)-distribution. The \(\alpha\)-quantile is denoted \(F_{\alpha,\,n,\,m}=1/F_{1-\alpha,\,m,\,n}\) and Figure 2.3D gives three examples of its density.

If \(X\sim\chi^2_n(\lambda)\) has a noncentral \(\chi^2\)-distribution, then \((X/n)/(Y/m)\sim F_{n,m}(\lambda)\) has a noncentral \(F\)-distribution with noncentrality parameter \(\lambda\). For \(m=\infty\), the \(F_{n,m}\)-distribution corresponds to the \(\chi^2_n\)-distribution \(\chi^2_n=F_{n,\infty}\), and for \(n=1\), the \(F\)-distribution corresponds to the square of a \(t\)-distribution \(F_{1,m}=t_m^2\). In the noncentral case, we have \(\chi^2_n(\lambda)=F_{n,\infty}(\lambda)\) and \(t_m(\eta)=F_{1,m}(\lambda=\eta^2)\).

2.2 Estimation

In practice, the expectation, variance, and other parameters of a distribution are often unknown and need to be determined from data, such as the ten measurements in Table 2.1. For the moment, we do not make assumptions on the distribution of these measured levels, and simply write \(Y_i\sim(\mu,\sigma^2)\) to emphasize that the observations \(Y_i\) have (unknown) mean \(\mu\) and (unknown) variance \(\sigma^2\). These two parameters should give us an adequate picture of the expected enzyme level and the variation in the mouse population.

The enzyme level \(y_i\) of mouse \(i\) will deviate from the population average \(\mu\) by a random amount \(e_i\) and we can write it as \[\begin{equation} y_i = \mu + e_i\;, \end{equation}\] where the deviations \(e_i\sim (0,\sigma^2)\) are distributed around a zero mean. There are two parts to this model: one part (\(\mu\)) describes the mean structure of our problem, that is, the location of the distribution; the other (\(e_i\) and the associated variance \(\sigma^2\)) the variance structure, that is, the deviations around the location. The deviations \(e_i=y_i-\mu\) are called residuals and capture the unexplained variation with residual variance \(\sigma^2\). The diagram in Figure 2.4 gives a visual representation of this situation: reading from top to bottom, it shows the increasingly finer partition of the data. On top, the factor M corresponds to the population mean \(\mu\) and gives the coarsest summary of the data. We write this factor in bold to indicate that its parameter is a fixed number. The summary is then refined by the next finer partition, which here already corresponds the ten individual mice. To each mouse is associated the difference from its average value (the observations \(y_i\)) and the next-coarser partition (the population mean) and the factor (Mouse) corresponds to the ten residuals \(e_i=\mu-y_i\). In contrast to the population mean, the residuals are random and will change in a repliation of the experiment. We indicate this fact by writing the factor in italic and parentheses.

The number of parameters associated with each granularity are given as a superscript (one population mean and ten residuals); the subscript gives the number of independent parameters. While there are ten residuals, there are only nine degrees of freedom for their values, since knowing nine residuals and the population mean allows calculation of the value for the tenth residual. The degrees of freedom are easily calculated from the diagram: take the number of parameters (the superscript) of each factor and subtract the degrees of freedom of every factor above it.

Since (Mouse) subdivides the partition of M into a finer partition of the data, we say that (Mouse) is nested in M.

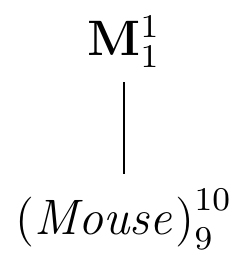
Figure 2.4: Experiment structure of enzyme levels from ten randomly sampled mice.

Our task is now three-fold: (i) provide an estimate of the expected population enzyme level \(\mu\) from the given data \(y_1,\dots,y_{10}\), (ii) provide an estimate of the population variance \(\sigma^2\), and (iii) quantify the uncertainty of our estimates.

The estimand is a population parameter \(\theta\) and an estimator of \(\theta\) is a function that takes data \(y_1,\dots,y_n\) as an input and returns a number that is a “good guess” of the true value of the estimand. For a given estimand, there might be several sensible estimators, and statistical theory and assumptions on the data usually provides insight into whcih estimator is most appropriate.

We denote an estimator of a parameter \(\theta\) by \(\hat{\theta}\) and sometimes use \(\hat{\theta}_n\) to emphasize its dependence on the sample size. The estimate is the value of \(\hat{\theta}\) that results from a specific set of data. Standard statistical theory provides us with methods for constructing estimators, such as least squares, which requires few assumptions, and maximum likelihood, which requires postulating the full distribution of the data but can then better leverage the data. Since the data are random, so is the estimate, and the estimator is therefore a random variable with an expectation and variance.

2.2.1 Properties of estimators

The bias of an estimator is the difference between its expectation and the true value of the parameter: \[ \text{bias}\left(\hat{\theta}\right) = \mathbb{E}\left(\hat{\theta}\right) - \theta = \mathbb{E}\left(\hat{\theta}-\theta\right)\;. \] We call an estimator unbiased if \(\text{bias}(\hat{\theta})=0\). Then, some realizations of our procedure will yield estimates that are larger than the true value, others will yield lower ones, but our estimator returns the correct parameter value on average. In contrast, a biased estimator systematically over- or underestimates the true parameter value. The extend of bias is sometimes also called the accuracy of the estimator and an estimator is accurate if it is unbiased.

While it is in general difficult to work out the full distribution of an estimator, the distribution of an estimator derived from the maximum likelihood principle tends to a normal distribution for large sample sizes such that \[ \frac{\hat{\theta}-\theta}{\text{sd}(\hat{\theta})}\sim N(0,1)\quad\text{for $n\to\infty$} \] for an unbiased maximum likelihood estimator.

An estimator is consistent if the estimates approach the true value of the parameter when increasing the sample size indefinitely and \[ \hat{\theta}_n \to \theta\quad\text{as $n\to\infty$}\;. \]

2.2.2 Estimators of expectation and variance

The most common estimator for the expectation \(\mu\) is the arithmetic mean \[ \hat{\mu} = \bar{y} = \frac{1}{n}\sum_{i=1}^n y_i\;. \] This estimator is unbiased, since \[ \mathbb{E}(\hat{\mu}) = \mathbb{E}\left(\frac{1}{n}\sum_{i=1}^n y_i\right)=\mu\;, \] and it is also consistent.

From the data in Table 2.1, for example, we find the estimate \(\hat{\mu}=\) 10.49 for a parameter value of \(\mu=\) 10.

Similarly, the maximum likelihood estimator for the variance is \[ \hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n (y_i-\mu)^2\;, \] but we would need \(\mu\) to calculate it. In order to make this estimator operational, we plug in the estimator \(\hat{\mu}\) instead of \(\mu\), which gives the estimator \[ \tilde{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n (y_i-\hat{\mu})^2\;. \] This estimator is biased and systematically underestimates the true variance: \[\begin{align*} \mathbb{E}(\tilde{\sigma}^2) &= \mathbb{E}\left(\frac{1}{n}\sum_{i=1}^n(y_i-\hat{\mu})^2\right) = \mathbb{E}\left(\frac{1}{n}\sum_{i=1}^n((y_i-\mu)-(\hat{\mu}-\mu))^2\right) \\ &= \frac{1}{n}\sum_{i=1}^n\left(\mathbb{E}((y_i-\mu)^2)-2\cdot\mathbb{E}(y_i-\mu)(\hat{\mu}-\mu)+\mathbb{E}((\hat{\mu}-\mu)^2)\right) \\ &= \frac{1}{n}\sum_{i=1}^n\left(\sigma^2-2\text{Cov}(y_i,\hat{\mu})+\frac{\sigma^2}{n}\right) = \frac{1}{n}\sum_{i=1}^n\left(\sigma^2-2\frac{\sigma^2}{n}+\frac{\sigma^2}{n}\right) \\ &= \left(\frac{n-1}{n}\right)\cdot\sigma^2 < \sigma^2\;. \end{align*}\] We remedy this bias by multiplying the estimator with \(\frac{n}{n-1}\) and thus arrive at an unbiased estimator for the variance \[\begin{equation} \hat{\sigma}^2 = \frac{n}{n-1}\tilde{\sigma}^2 = \frac{1}{n-1}\sum_{i=1}^n (y_i-\hat{\mu})^2\;. \end{equation}\] Note that the denominator \(n-1\) corresponds exactly to the degrees of freedom for the residuals in the diagram (Fig. 2.4).

An estimator for the standard deviation \(\sigma\) is \(\hat{\sigma}=\sqrt{\hat{\sigma}^2}\); this estimator is biased and no unbiased estimator for \(\sigma\) exists.

For our example, we find that the biased estimator is \(\tilde{\sigma}^2=\) 3.39 and the unbiased estimator is \(\hat{\sigma}^2=\) 3.77 (for \(\sigma^2=\) 2); the estimate of the standard deviation is then \(\hat{\sigma}=\) 1.94 (for \(\sigma=\) 1.41).

With the same arguments, we find that \[ \widehat{\text{Cov}}(X,Y) = \frac{1}{n-1}\sum_{i=1}^n\left((x_i-\hat{\mu}_X)\cdot(y_i-\hat{\mu}_Y)\right) \] is an estimator of the covariance \(\text{Cov}(X,Y)\) of two random variables \(X\) and \(Y\) with means \(\mu_X\) and \(\mu_Y\), based on two samples (of equal size) \(x_1,\dots,x_n\) and \(y_1,\dots,y_n\). Combining this with the estimates of the standard deviations yields an estimator for the correlation \(\rho\) of \[ \hat{\rho} = \frac{\widehat{\text{Cov}}(X,Y)}{\widehat{\text{sd}}(X)\cdot\widehat{\text{sd}}(Y)}\;. \]

For our two-sample example, we find a covariance between first and second sample of \(\widehat{\text{Cov}}(Y_{i,1},Y_{i,2})=\) 3.47 and thus a very high correlation of \(\hat{\rho}=\) 0.99.

2.2.3 Standard error and precision

Since an estimator \(\hat{\theta}\) is a random variable, it has a variance \(\text{Var}(\hat{\theta})\), which quantifies the dispersion around its mean. In general, this dispersion decreases with increasing sample size. The standard deviation \(\text{sd}(\hat{\theta})\) is called the standard error of the estimator and denoted \(\text{se}(\hat{\theta})\). We call its reciprocal \(1/\text{sd}(\hat{\theta})\) the precision.

The estimator \(\hat{\mu}\) has a normal distribution with variance \(\text{Var}(\hat{\mu})=\sigma^2/n\) for normally distributed data. Its standard error is \[ \text{se}(\hat{\mu})=\sigma/\sqrt{n} \] and decreases with rate \(1/\sqrt{n}\) when increasing the sample size \(n\). For doubling the precision, we require four times the amount of data, and to get one more digit of the estimate precise, we need to increase our sample a hundred-fold. The standard error depends on the unknown variance of the data, we estimate it by plugging in an estimate of \(\sigma^2\): \[ \widehat{\text{se}}(\hat{\mu})=\hat{\sigma}/\sqrt{n}\;. \] For our example, we find that \(\widehat{\text{se}}(\hat{\mu})=\) 0.61 and the standard error is only about 6% of the estimated expectation \(\hat{\mu}=\) 10.32.

For normally distributed data, the ratio \[ \frac{\hat{\sigma}^2}{\sigma^2} = \frac{1}{n}\sum_{i=1}^n \left(\frac{y_i-\mu}{\sigma}\right)^2\;. \] has a \(\chi^2\)-distribution. To compensate for the larger uncertainty when using an estimate \(\hat{\mu}\) instead of the true value, we need to adjust the degrees of freedom and arrive at the distribution of the variance estimator \(\hat{\sigma}^2\): \[ \frac{(n-1)\hat{\sigma}^2}{\sigma^2}\sim\chi^2_{n-1}\;. \] This distribution has variance \(2(n-1)\), and from it we find the variance of the estimator to be \[ 2(n-1)=\text{Var}\left(\frac{(n-1)\hat{\sigma}^2}{\sigma^2}\right)=\frac{(n-1)^2}{\sigma^4}\text{Var}(\hat{\sigma}^2) \iff \text{Var}(\hat{\sigma}^2)=\frac{2}{n-1}\sigma^4\;, \] and \(\text{se}(\hat{\sigma}^2)=\sqrt{2/(n-1)}\sigma^2\). Again, this means doubling the precision requires four times as much data. The standard error also now depends on the true variance, and larger variances are more difficult to estimate precisely and smaller variances.

For our example, we find the variance estimate \(\hat{\sigma}^2=\) 3.77 has an estimated standard error of \(\widehat{\text{se}}(\hat{\sigma}^2)=\) 1.78. This is thus an example of an accurate (unbiased) yet imprecise estimator. Indeed, the precision and accuracy of an estimator are complementary properties as illustrated in Figure 2.5: the precision describes the dispersion of estimates around the expected value while accuracy describes the systematic deviation between expectation and true value. Estimates might cluster very closely around a single value, indicating high precision, yet estimates might still be incorrect for a biased estimator, when this single value is not the parameter value.

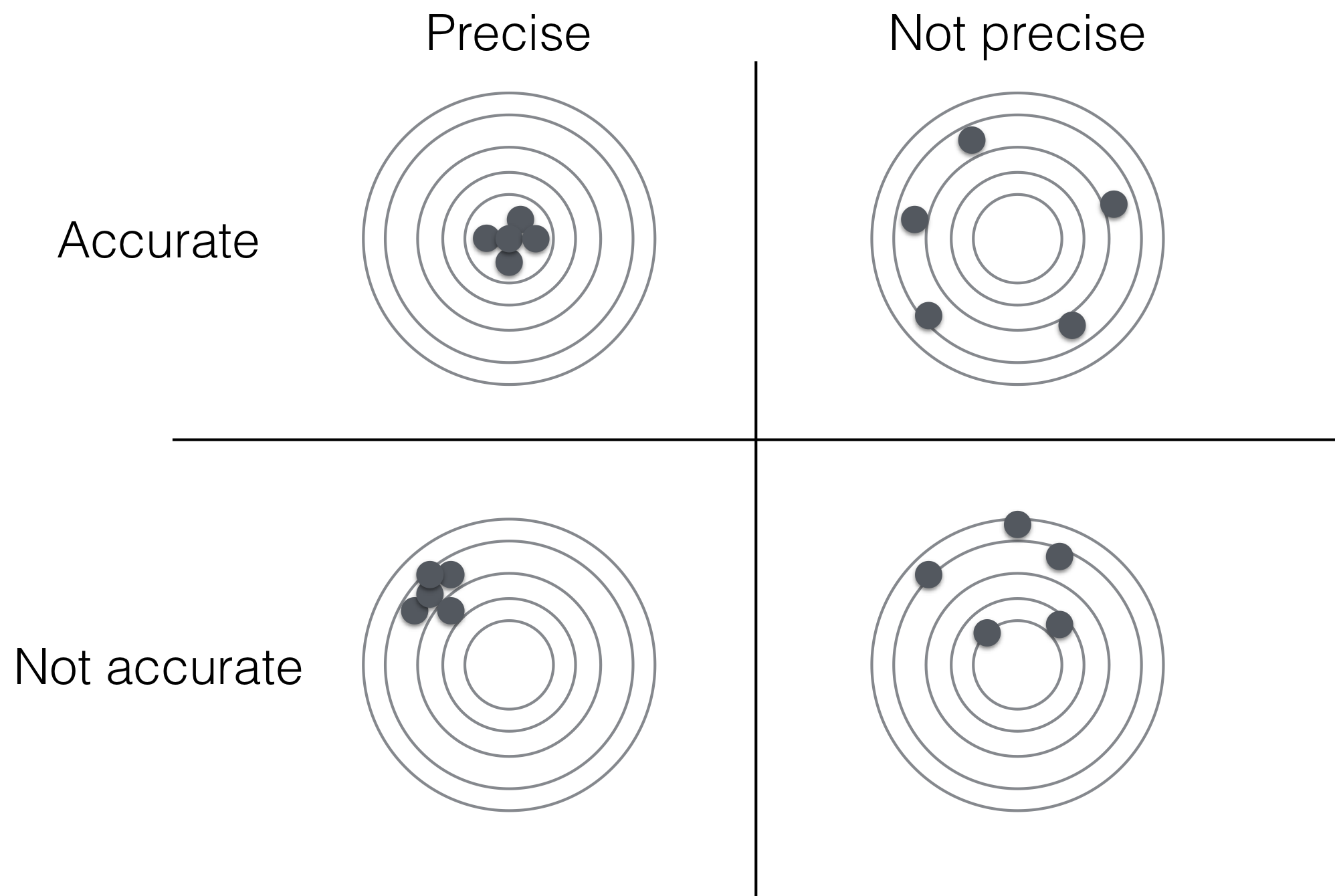
Figure 2.5: Difference between accuracy and precision of estimator

2.2.4 Confidence intervals

The estimators for expectation and variance are examples of point estimators and provide a single number as the ``best guess’’ of the true parameter from the data. The standard error or precision quantify the uncertainty of a point estimate and immediately show that an estimate of the average enzyme level based on one hundred mice is less uncertain than an estimate based on only two mice.

A confidence interval of a parameter \(\theta\) is another way for quantifying the uncertainty that additionally takes account of the full distribution of the estimator. The interval contains all possible values of the parameter that are compatible with the observed data up to a specified degree. The \((1-\alpha)\)-confidence interval of an estimator \(\hat{\theta}\) is an interval \([a(\hat{\theta)},b(\hat{\theta})]\) such that \[ \mathbb{P}\left(a(\hat{\theta})\leq \theta \leq b(\hat{\theta})\right) = 1-\alpha\;. \] We call the values \(a(\hat{\theta})\) and \(b(\hat{\theta})\) the lower and upper confidence limit, respectively, and sometimes abbreviate them as LCL and UCL. The confidence level \(1-\alpha\) quantifies the degree of being ‘compatible with the data’. The higher the confidence level (the lower \(\alpha\)), the wider the interval, until a 100%-confidence interval includes all possible values of the parameter and becomes useless.

While not strictly required, we always choose the confidence limits \(a\) and \(b\) such that the left and right tail each cover half of the required confidence level. This provides the shortest possible confidence interval.

The confidence interval equation is a probability statement about a random interval covering \(\theta\) and not a statement about the probability that \(\theta\) is contained in a given interval. For example, it is incorrect to say that, having computed a 95%-confidence interval of \([-2, 2]\), the true population parameter has a 95% probability of being larger than \(-2\) and smaller than \(+2\). Such a statement would be nonsensical, because any given interval either contains the true value (which is a fixed number) or it does not, and there is no probability attached to this.

One correct interpretation is that the proportion of intervals containing the correct value \(\theta\) is a\((1-\alpha)\) under repeated sampling and estimation. This interpretation is helpful in contexts like quality control, where the ‘same’ experiment is done repeatedly and there is thus a direct interest in the proportion of intervals containing the true value. For most biological experiments, we do not anticipate repeating them over and over again. Here, an equivalent interpretation is that our specific confidence interval, computed from the data of our experiment, has a \((1-\alpha)\) probability to contain the correct parameter value.

For computing a confidence interval, we need to know the distribution of the estimator. For maximum likelihood estimators, we know that at least asymptotically for large sample sizes, \[ \frac{\theta-\hat{\theta}}{\text{se}(\hat{\theta})} \sim N(0,1)\;, \] and therefore that \[ \mathbb{P}\left(z_{\alpha/2}\leq \frac{\theta-\hat{\theta}}{\text{se}(\hat{\theta})} \leq z_{1-\alpha/2}\right) = 1-\alpha\;, \] where \(z_\alpha\) is the \(\alpha\)-quantile of the standard normal distribution. Rearranging terms yields the well-known confidence interval for an unbiased maximum likelihood estimator \[ \left[ \hat{\theta}+z_{\alpha/2}\cdot\text{se}(\hat{\theta}),\; \hat{\theta}+z_{1-\alpha/2}\cdot\text{se}(\hat{\theta}) \right]\;. \] For some standard estimators, the exact distribution might not be normal, but is nevertheless known. If the distribution is not known or difficult to compute, then computational methods such as the bootstrap can be used to find an approximate confidence interval.

2.2.4.1 Confidence interval for mean estimate

For normally distributed data \(y_i\sim N(\mu,\sigma^2)\), we known that \[ \frac{\hat{\mu}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) \quad\text{and}\quad \frac{\hat{\mu}-\mu}{\hat{\sigma}/\sqrt{n}}\sim t_{n-1} \;. \] From this, we find a theoretical \((1-\alpha)\)-confidence interval of \[ \left[ \hat{\mu}+z_{\alpha/2}\cdot\frac{\sigma}{\sqrt{n}},\; \hat{\mu}+z_{1-\alpha/2}\cdot\frac{\sigma}{\sqrt{n}} \right] = \hat{\mu}\pm z_{\alpha/2}\cdot\frac{\sigma}{\sqrt{n}}\;, \] where the equality holds because \(z_{\alpha/2}=-z_{1-\alpha/2}\). For small sample sizes \(n\), we need to take account of the additional uncertainty from replacing \(\sigma\) by \(\hat{\sigma}\). The exact confidence interval of \(\mu\) is then \[ \hat{\mu}\pm t_{\alpha/2,\,n-1}\cdot\widehat{\text{se}}(\hat{\mu}) = \hat{\mu}\pm t_{\alpha/2\,n-1}\cdot \hat{\sigma}/\sqrt{n}\;. \]

For our data, the 95%-confidence interval based on the normal approximation is [9.8, 11.2] and the interval based on the \(t\)-distribution is [9.7, 11.2]; the \(t\)-interval is wider, since it takes account of the additional uncertainty introduced by using an estimate for the standard error. For larger samples sizes \(n\), the difference between the two intervals quickly becomes negligible.

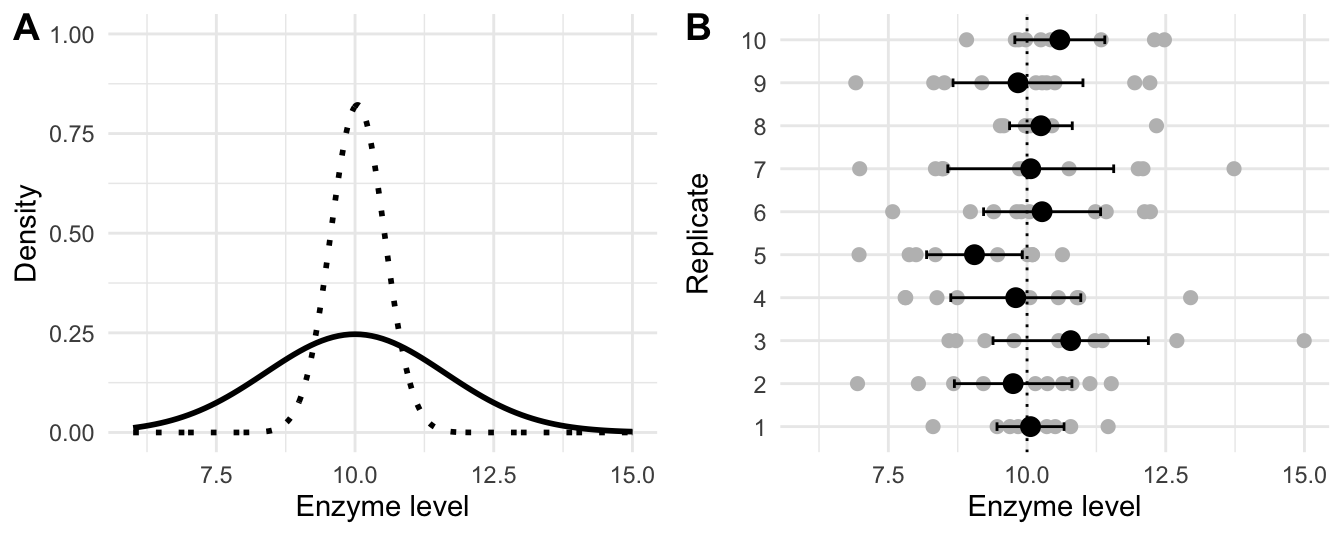
Figure 2.6: A: distribution of enzyme levels in population (solid) and of average (dotted); B: levels measured for ten replicates of ten randomly sampled mice each (grey points) with estimated mean for each replicate (black points) and their 95% confidence intervals (black lines) compared to true mean (dotted line).

To further illustrate what confidence intervals are and how they depend on sample size, we return to our enzyme level example. The true \(N(10,2)\)-density of enzyme levels is shown in Figure 2.6A (solid line) and the \(N(10,2/10)\)-density of the estimator of the expectation based on ten samples is shown as a dotted line. The rows of Figure 2.6B show the enzyme levels of ten replicates of ten randomly sampled mice as grey points, with the true average \(\mu=\) 10 shown as a vertical dotted line. The resulting estimates of the expectation and their 95%-confidence intervals are shown as black points and lines, respectively. The ten estimates vary much less than the actual measurements and fall both above and below the true expectation. Since the confidence intervals are based on the random samples, they have different lower and upper confidence limits and different lengths. For a confidence limit of 95% we expect that 1 out of 20 confidence intervals does not to cover the true value on average; an example is the interval of replicate five that covers only values below the true expectation.

2.2.4.2 Confidence interval for variance estimate

For the variance estimator, recall that \((n-1)\hat{\sigma}^2/\sigma^2\) has a \(\chi^2\)-distribution. It follows that \[ \chi^2_{\alpha/2,\,n} \leq \frac{(n-1)\hat{\sigma}^2}{\sigma^2}\leq \chi^2_{ 1-\alpha/2,\,n-1}\quad\text{with probability $1-\alpha$}\;, \] where \(\chi^2_{\alpha,\,n}\) is the \(\alpha\)-quantile of a \(\chi^2\)-distribution with \(n\) degrees of freedom. Rearranging terms, we find the \((1-\alpha)\)-confidence interval \[ \frac{(n-1)\hat{\sigma}^2}{\chi^2_{1-\alpha/2,\,n-1}} \leq \sigma^2 \leq \frac{(n-1)\hat{\sigma}^2}{\chi^2_{\alpha/2,\,n-1}}\;. \] This interval does not simplify to the form \(\hat{\theta}\pm q_\alpha\cdot \text{se}\), because the \(\chi^2\)-distribution is not symmetric and \(\chi^2_{\alpha,\,n}\not=-\chi^2_{1-\alpha,\,n}\).

For our example, we estimate the population variance as \(\hat{\sigma}^2=\) 3.77 (for a true value of \(\sigma^2=\) 2). With \(n-1=\) 9 degrees of freedom, the two quantiles for a 95%-confidence interval are \(\chi^2_{0.025,\,9}=\) 2.7 and \(\chi^2_{0.975,\,9}=\) 19.02, leading to an interval of [0.95, 6.67]. The interval covers the true value, but its width indicates that our variance estimate is quite imprecise. A confidence interval for the standard deviation \(\sigma\) is calculated by taking square-roots of the lower and upper confidence limits of the variance. This yields a 95%-confidence interval of [0.97, 2.58] for our estimate \(\hat{\sigma}=\) 1.94 (true value of \(\sigma=\) 1.41).

2.2.5 Estimation for comparing two samples

Commonly, we are interested in comparing properties of two different samples to determine if there are detectable differences between their distributions. For example, if we always used a sample preparation kit of vendor A for our enzyme level measurements, but vendor B now also has a (maybe cheaper) kit available, we may want to establish if the two kits yield similar results. For this example, we are specifically interested in establishing if there is a systematic difference between measurements based on kit A compared to kit B and if measurements from one kit are more dispersed than from the other kit.

We denote by \(\mu_A, \mu_B\) the expectations and by \(\sigma^2_A, \sigma^2_B\) the variances of the enzyme levels \(y_{i,A}\) and \(y_{i,B}\) measured by kit A and B, respectively. Our interest focusses on two effect sizes: we measure the systematic difference between the kits by the difference \(\Delta=\mu_A-\mu_B\) in their expected values, and we measure the difference in variances by their proportion \(\Pi=\sigma_A^2/\sigma_B^2\). Since we already have ten measurements with our standard kit A, our proposed experiment is to select another ten mice and measure their levels using kit B. This results in the data shown in Table 2.3, whose first row is identical to our previous data.

Table 2.3: Measured enzyme levels for 20 mice, measured by kits from two vendors A and B.

A	8.96	8.95	11.37	12.63	11.38	8.36	6.87	12.35	10.32	11.99
B	12.68	11.37	12.00	9.81	10.35	11.76	9.01	10.83	8.76	9.99

Our goal is to establish how to estimate the difference in means, the proportion of variances and—more importantly—how to calculate appropriate confidence intervals for these estimates.

The logical structure of the experiment is shown in the diagram in Figure 2.7. The data from this experiment are described by the common mean \(\mu=(\mu_A+\mu_B)/2\), given by the factor M; this is the ‘best guess’ for the value of any datum \(y_{ij}\) if nothing else is known. If we know which vendor was assigned to the datum, a better ‘guess’ is the corresponding mean \(\mu_A\) or \(\mu_B\). The factor Vendor is associated with the two differences between \(\mu_A-\mu\) and \(\mu-\mu_B\). Since we can calculate \(\mu_A\), say, from \(\mu\) and \(\mu_B\), the degrees of freedom for this factor are one. Finally, the next finer partition of the data is into the individual observations; their \(2\cdot 10\) residuals \(e_{ij}=y_{ij}-\mu_i\) are associated with the factor (Mouse), and only 18 of the residuals are independent given the two group means. In this diagram, (Mouse)is nested in Vendor and Vendor is nested in M since each factor further subdivides the partition of the factor above. This implies that (Mouse) is also nested in M.

The diagram corresponds to the model \[ y_{ij} = \mu + \delta_i + e_{ij}\;, \] for the data, where \(\delta_i=\mu-\mu_i\) are the deviations from population mean to group mean and \(\mu_A=\mu+\delta_A\) and \(\mu_B=\mu+\delta_B\). The three parameters \(\mu\), \(\delta_A\) and \(\delta_B\) are unknown but fixed quantities, while the \(e_{ij}\) are random and interest focusses on their variance \(\sigma^2\).

Figure 2.7: Experiment for estimating the difference in enzyme levels by randomly assigning 10 mice each to two vendors.

2.2.5.1 Proportion of variances

For two normally distributed samples of size \(n\) and \(m\), respectively, we estimate the proportion of variances as \(\hat{\Pi}=\hat{\sigma}^2_A/\hat{\sigma}^2_B\). We derive a confidence interval for this estimator by noting that \((n-1)\hat{\sigma}_A^2/\sigma_A^2\sim\chi^2_{n-1}\) and \((m-1)\hat{\sigma}_B^2/\sigma_B^2\sim\chi^2_{m-1}\). Then, \[ \frac{\frac{(n-1)\hat{\sigma}_A^2}{\sigma_A^2}/(n-1)} {\frac{(m-1)\hat{\sigma}_B^2}{\sigma_B^2}/(m-1)} =\frac{\hat{\sigma}_A^2/\sigma_A^2}{\hat{\sigma}_B^2/\sigma_B^2} =\frac{\hat{\Pi}}{\Pi}\sim F_{n-1,m-1} \] has an \(F\)-distribution with \(n-1\) numerator and \(m-1\) denominator degrees of freedom. A \((1-\alpha)\)-confidence interval for \(\Pi\) is therefore \[ \left[\frac{\hat{\Pi}}{F_{1-\alpha/2,\,n-1,\, m-1}},\,\frac{\hat{\Pi}}{F_{\alpha/2,\,n-1,\, m-1}}\right]\;. \] For our example, we find the two individual estimates \(\hat{\sigma}^2_A=\) 3.77 and \(\hat{\sigma}^2_B=\) 1.69 and an estimated proportion \(\hat{\Pi}=\) 2.23. This yields a 95%-confidence interval for \(\hat{\Pi}\) of [0.55, 8.98]. Given the data, both ratios below and above one are plausible and we have no reason to assume that the two true variances are substantially different, even though their two estimators differ by a factor larger than 2.

2.2.5.2 Difference in means of independent samples

We estimate the systematic difference \(\Delta\) between the two kits using the difference between the estimates of the respective expected enzyme levels: \[ \hat{\Delta}=\widehat{\mu_A-\mu_B} = \hat{\mu}_A-\hat{\mu}_B\;. \] For the example, we estimate the two average enzyme levels as \(\hat{\mu}_A=\) 10.32 and \(\hat{\mu}_B=\) 10.66 and the difference as \(\hat{\Delta}=\) -0.34. The estimated difference is not exactly zero, but this might be explainable by measurement error or the natural variation of enzyme levels between mice.

We take account of the uncertainty by calculating the standard error and a 95%-confidence interval for \(\hat{\Delta}\). The lower and upper confidence limits then provide information about a potential systematic difference: if the upper limit is below zero, then only negative differences are compatible with the data, and we can conclude that measurements of kit A are systematically lower than measurements of kit B. Conversely, a lower limit above zero indicates kit B yielding systematically higher values than kit A. If zero is contained in the confidence interval, we cannot determine the direction of a potential difference, and it is also plausible that no difference exists.

We already established that the data provides no evidence against the assumption that the two variances are equal. We therefore assume a common variance \(\sigma^2=\sigma^2_A=\sigma^2_B\), which we estimate by the pooled variance estimate \[ \hat{\sigma}^2 = \frac{\hat{\sigma}_A^2+\hat{\sigma}_B^2}{2}\;. \] For our our data, \(\hat{\sigma}^2=\) 2.73 and the estimated standard deviation is \(\hat{\sigma}=\) 1.65.

Compared to this standard deviation, the estimated difference is small (about 21%). Whether such a small difference is meaningful in practice depends on the subject matter. A helpful dictum is

A difference that makes no difference is not a difference.

To determine the confidence limits, we first need the standard error of the difference estimate. The two estimates \(\hat{\mu}_A\) and \(\hat{\mu}_B\) are based on independently selected mice, and are therefore independent. Simple simple application of the rules for variances then yields: \[ \text{Var}(\hat{\Delta}) = \text{Var}(\hat{\mu}_A-\hat{\mu}_B) = \text{Var}(\hat{\mu}_A)+\text{Var}(\hat{\mu}_B)=2\cdot\frac{\sigma^2}{n}\;. \] The standard error of the difference estimator is therefore \[ \widehat{\text{se}}(\hat{\Delta}) = \sqrt{2\cdot\frac{\hat{\sigma}^2}{n}}\;, \] which yields \(\widehat{\text{se}}(\hat{\Delta})=\) 0.74 for our data.

Using the same arguments as before, an \((1-\alpha)\)-confidence interval for \(\Delta\) is \[ \hat{\Delta} \pm t_{\alpha/2,\,2n-2}\cdot \widehat{\text{se}}(\hat{\Delta}) \quad=\quad(\hat{\mu}_A-\hat{\mu}_B) \pm t_{\alpha/2,\,2n-2}\cdot \sqrt{2\cdot\frac{\hat{\sigma}^2}{n}}\;. \] Note that we have \(2n\) observations in total, from which we estimate the two means, resulting in \(2n-2\) degrees of freedom for the \(t\)-distribution. Note again that these are the degrees of freedom of the factor (Mouse) in Figure 2.7.

For our data, we calculate a 95%-confidence interval of [-1.89, 1.21]. The confidence interval contains the value zero, and two kits might indeed produce equivalent values. The interval also contains negative and positive values of substantial magnitude that are possibly relevant in practice. From the data, we can therefore only conclude that there is no evidence of a systematic difference between kits, but if such difference existed, it might be large enough to be practically relevant.

2.2.5.3 Difference in means of dependent samples

As a second illustration, we consider our data of ten mice with two measured samples each (Table 2.2). With \(y_{i,j}\) the observed level of the \(j\)th sample of mouse \(i\), the estimators for the two individual means and variances of the first and second samples are \(\hat{\mu}_j=\sum_{i=1}^n y_{i,j}/n\) and \(\hat{\sigma}_j^2=\sum_{i=1}^n (y_{i,j}-\hat{\mu}_j)^2/(n-1)\). In contrast to the previous example, each pair of two samples is correlated, since they are taken from the same mouse. An estimate of the difference \(\Delta'=\mu_1-\mu_2\) is then \[ \hat{\Delta}'=\frac{1}{n}\sum_{i=1}^n (y_{i,1}-y_{i,2})=\frac{1}{n}\sum_{i=1}^n y_{i,1}-\frac{1}{n}\sum_{i=1}^n y_{i,2}=\hat{\mu}_1-\hat{\mu}_2\;. \] This is the same estimator as for two independent samples. However, its variance is very different because of the non-zero covariance between two samples from the same mouse: \[ \text{Var}(\hat{\mu}_1-\hat{\mu}_2)=\frac{\text{Var}(\hat{\mu}_1)}{n}+\frac{\text{Var}(\hat{\mu}_2)}{n}-2\frac{\text{Cov}(\hat{\mu}_1,\hat{\mu}_2)}{n} =2\frac{\sigma_m^2+\sigma_e^2}{n}-2\frac{\sigma_m^2}{n}=2\frac{\sigma_e^2}{n}\;. \] For the data in Table 2.2, we find estimates \(\hat{\mu}_1=\) 10.32, \(\hat{\mu}_2=\) 10.49, \(\hat{\sigma}^2_1=\) 3.77, \(\hat{\sigma}^2_2=\) 3.26, and \(\widehat{\text{Cov}}(y_{i,1},y_{i,2})=\) 3.47. The estimate for the difference in means is then \(\hat{\Delta}'=\) -0.17 with a standard error of \(\widehat{\text{se}}(\hat{\Delta}')=\) 0.09. This standard error is much lower than for the two vendor example, even though the individual variances of the first and second samples are comparable to each other and to the variances in our other examples. This is due to the covariance between the two samples in this example, which removes the mouse-to-mouse variation \(\sigma_m^2\) (recall that we decomposed \(\sigma^2\) into \(\sigma_m^2+\sigma_e^2\) and \(\sigma_m^2\) is much larger that \(\sigma_e^2\)): the estimate of the difference is based on the individual differences between first and second sample for each mouse. These individual differences are not subject to mouse-to-mouse variation, since they are taken from data of the same mouse.

The \((1-\alpha)\)-confidence interval is \[ \hat{\Delta}'\pm t_{\alpha/2,n-1}\cdot\text{se}(\hat{\Delta}')\;, \] and is based on \(n-1=\) 9 degrees of freedom (note that we have a single sum with 10 summands, not two independent sums!). The 95%-confidence interval for our data is [-0.38, 0.04] and is much narrower again than for the previous example which might allow stronger conclusions. For example, if absolute differences below 0.5 are not biologically meaningful, then the narrow confidence interval contains no difference of relevant magnitude and we can be confident that no systematic difference between first and second sample exists.

The experiment is illustrated in Figure 2.8. In contrast to the previous diagrams, the structure of this design is no longer a chain of nested factors, since the dataset can be partitioned in two independent ways: either into one subset per vendor, which is then summarized by the group means \(\delta_j=\mu_j-\mu\), or by the mice, summarized by the average response \(\mu+m_i\) per mouse. The two factors (Mouse) and Vendor are crossed, and an sample observation is available for each combination of mouse and vendor kit. We denote the crossing by writing the factors next to each other without a connecting edge. Each sample is thus associated with one mouse and one vendor, and the corresponding factor is nested in both. Since the mice are randomly selected, their average responses are also random (\(m_i\) is a random variable), and \(\sigma_m^2\) is the corresponding variance of the deviation from a mouse average to the grand mean \(\mu\). A model for the observations in this experiment is \[ y_{ij} = \mu + \delta_j + m_i + e_{ij}\;, \] and \(\mathbb{E}(y_{ij})=\mu+\delta_j\) while \(\text{Var}(y_{ij})=\sigma_m^2+\sigma_e^2\).

Figure 2.8: Paired design for estimating average enzyme level difference: 10 mice, each vendor assigned to one of two samples per mouse.

Standardized effect size for difference

The difference \(\Delta\) is an example of a raw effect size and measures the difference in the same units as the original measurements. Subject-matter knowledge often provides information about the relevance of specific effect sizes and might tell us, for example, that a difference in enzyme levels of more than 1.5 is biologically relevant.

Sometimes the raw effect size is difficult to interpret. This is a particular problem with some current measurement techniques in biology, which give measurements in arbitrary units (a.u.), making it difficult to directly compare results from two experiments. In this case, a unit-less standardized effect size might be more appropriate. These are popular in fields like psychology and social sciences, but have also been advocated for biological research (Nakagawa and Cuthill 2007). A popular choice for a difference is Cohen’s \(d\), which compares the difference with the standard deviation in the population: \[ d = \frac{\mu_A-\mu_B}{\sigma} \quad\text{estimated by}\quad \hat{d} = \frac{\hat{\mu}_A-\hat{\mu}_B}{\hat{\sigma}}\;. \] It is a unit-less effect size that measures the raw difference a a multiple of the standard deviation. If \(|d|=1\), then the two means are one standard deviation apart. In the original literature, Cohen suggests that \(|d|<0.2\) should be considered a small effect, \(0.2<|d|<0.5\) a medium-sized effect, and \(0.5<|d|<0.8\) a large effect (Cohen 1988), but such definitive categorization should not be taken too literally.

For our example, we calculate \(\hat{d}=\) -0.21, a difference of about 21% standard deviations, indicating a small-to-medium effect size. The exact confidence interval for \(\hat{d}\) is based on a non-central \(t\)-distribution and cannot be given in closed form. For large enough sample size, we can use a normal approximation interval \(\hat{d}\pm z_{1-\alpha/2}\cdot\widehat{\text{se}}(\hat{d})\) based on an approximation of the standard error (Hedges and Olkin 1985): \[ \widehat{\text{se}}(\hat{d}) = \sqrt{ \frac{n_A+n_B}{n_A\cdot n_B}+\frac{\hat{d}^2}{2\cdot(n_A+n_B)} }\;, \] where \(n_A\) and \(n_B\) are the respective sample sizes for the two groups. For our example, this yields an approximate 95%-confidence interval of [-1.08, 0.67].

2.3 Testing hypotheses

The underlying question in our kit vendor example is whether the statement \(\mu_A=\mu_B\) about the true underlying parameters is true or not. We argued that the data would not support this statement if the confidence interval of \(\Delta\) lies completely above or below zero, excluding \(\Delta=0\) as a plausible parameter value. Significance testing is an equivalent way of using the observations for evaluating the evidence in favor or against a specific null hypothesis, such as \[ H_0: \mu_A=\mu_B \quad\text{or equivalently}\quad H_0: \Delta=0\;. \] The null hypothesis is a statement about the true value of one or more parameters.

2.3.1 The logic of falsification

Testing hypotheses follows a logic closely related to that of scientific research in general: we start from a scientific conjecture or theory to explain a phenomenon. From the theory, we derive observable consequences (or predictions) that we test in an experiment. If the predicted consequences are in substantial disagreement with those experimentally observed, then the theory is deemed implausible and is rejected or falsified. If, on the other hand, prediction and observation are in agreement, then the experiment failed to reject the theory. However, this does not mean that the theory is proven or verified since the agreement might be due to chance, the experiment not specific enough, or the data too noisy to provide sufficient evidence against the theory.

It is instructive to explicitly write down this logic more formally. The correctness of the conjecture \(C\) implies the correctness of the prediction \(P\): \[ C \text{ true}\implies P\text{ true}\;. \] We say \(C\) is sufficient for \(P\). We now perform an experiment to determine if \(P\) is true. If the experiment supports \(P\), we did not gain much, since we cannot invert the implication and conclude that the conjecture \(C\) must also be true. Many other possible conditions might lead to the predicted outcome that have nothing to do with our conjecture.

However, if the experiment shows the prediction \(P\) to be false, then we can invoke the modus tollens \[ P \text{ false} \implies C\text{ false} \] and conclude that \(C\) cannot be true. We say \(P\) is necessary for \(C\). There is thus an asymmetry in the relation of ’‘\(P\) is true’’ and ’‘\(P\) is false’’ towards the correctness of \(C\), and we can falsify a theory (at least in principle), but never fully verify it. The philosopher Karl Popper argued that falsification is a cornerstone of science and falsifiability (in principle) of conjectures separates a scientific theory from a non-scientific one (Popper 1959).

Statistical testing of hypotheses follows a similar logic, but adds a probabilistic argument to quantify the (dis-)agreement between hypothesis and observation. The data may provide evidence to reject the null hypothesis, but can never provide evidence for accepting the null hypothesis. We therefore formulate a null hypothesis for the ‘undesired’ outcome such that if we don’t reject it, nothing is gained and we don’t have any clue from the data how to proceed in our investigation. If the data provides evidence to reject the hypothesis, however, we can reasonably exclude it as a possible explanation of the observed data.

To appraise the evidence that our data provides for or against the null hypothesis, we need to take the random variation in the data into account. Instead of a yes/no answer, we can then only argue that “if the hypothesis is true, then it is (un-)likely that data like ours would be observed”. This is precisely the argument from the hypothesis to the observable consequences, but with a probabilistic twist.

2.3.2 The \(t\)-test

For our example, we know that if the true difference \(\Delta\) is zero, then the estimated difference \(\hat{\Delta}\) divided by its standard error has a \(t\)-distribution. This motivates the well-known T-statistic \[\begin{equation} T = \frac{\hat{\Delta}}{\widehat{\text{se}}(\hat{\Delta})} = \frac{\hat{\Delta}}{\sqrt{2\cdot \hat{\sigma}^2/n}} \sim t_{2n-2}\;. \tag{2.1} \end{equation}\]

Thus, our conjecture is “the null hypothesis is true and \(\Delta=0\)” from which we derive the prediction “the observed test statistic \(T\) based on the two sample averages follows a \(t\)-distribution with \(2n-2\) degrees of freedom”.

For our data, we compute a \(t\)-statistic of \(t=\) -0.65, based on the two means 10.32 for vendor A, 10.66 for vendor B, their difference -0.34, and the resulting standard error of 0.52 of the difference on 38 degrees of freedom. The estimated difference in means is expressed by \(t\) as about 65% of a standard error, and the sign of \(t\) indicates that measurements with kit A might be lower than with kit B.

2.3.3 \(p\)-values and statistical significance

\(p\)-values

From the distribution of our test statistic \(T\) under the assumption that the hypothesis \(H_0\) is true, we can compute the probability that \(T\) exceeds any given value in either direction. Calculating this probability at the observed value \(t\) provides us with a quantitative measure of the evidence that our data provides against the hypothesis. This probability is called the \(p\)-value \[ p = \mathbb{P}_{H_0}(|T|\geq |t|)\;. \] Because our test statistic is random (it is a function of the random samples), the \(p\)-value is also a random variable. If the null hypothesis is true, then \(p\) has a uniform distribution between \(0\) and \(1\).

For our example, we compute a \(p\)-value of 0.52, and we expect a \(t\)-statistic that deviates from zero by 0.65 or more in either direction in 52 out of 100 cases whenever the null hypothesis is true. We conclude that based on the variation in the data and the sample size, a difference of at least this magnitude is very likely and there is no evidence against the null hypothesis in the data.

A low \(p\)-value is considered indicative of \(H_0\) being false, since it is unlikely that such an extreme observed value for the test statistic would occur if the hypothesis were true. This leads to a dichotomy of explanations for small \(p\)-values: either an exceptionally rare chance has occurred, or the theory of random distribution is not true (Fisher 1956); here ‘random distribution’ refers to the distribution of \(T\) under the null hypothesis. On the other hand, a large \(p\)-value might occur because either \(H_0\) is true or because \(H_0\) is false but our data did not yield sufficient information to detect the true difference in means.

If possible, we should always combine an argument based on a \(p\)-value with the observed effect size: a test result is only meaningful if we find both a low \(p\)-value (indicating that the effect found can be distinguished from noise) and the observed effect size is practically relevant. Even a large effect size might yield a large \(p\)-value if the test has low power and the standard error is large. In our case, the estimated difference of \(\hat{\Delta}=\) -0.34 is small compared to the standard error \(\widehat{\text{se}}(\hat{\Delta})=\) 0.52 and cannot be distinguished from random fluctuation. That our test does not provide evidence for a difference does not mean it does not exist, however:

Absence of evidence is not evidence of absence.

We may decide to ignore a large \(p\)-value and still move ahead and assume that \(H_0\) is wrong; but the argument for so doing cannot rest on the single experimental result and its statistical analysis, but must include external arguments such as subject-matter considerations (e.g., about plausible effects) or outcomes of related experiments.

Conversely, a low \(p\)-value means that we were able to separate the observed difference from a random fluctuation, but the detected difference might have a tiny and irrelevant effect size if random variation is low or sample sizes big. However, this provides only one (crucial) piece of the argument why we suggest a particular interpretation and rule out others and does not excuse us from proposing a reasonable interpretation of the whole investigation and other experimental data.

Statistical significance

We sometimes use a pre-defined significance level \(\alpha\) against which we compare the \(p\)-value. If \(p<\alpha\), then we consider the \(p\)-value low enough to reject the null-hypothesis and we call the test statistically significant. The hypothesis is not rejected otherwise, a result called not significant. The level \(\alpha\) codifies our judgement of what constitutes an ‘exceptionally rare chance’. There is no theoretical justification for any choice of this threshold, but for as much historical as practical reasons, values of \(\alpha=5\%\) or \(\alpha=1\%\) are commonly used. Both thresholds are far exceeded in our example, and the test outcome is thus deemed not significant. The significance level is the probability to incorrectly rejecting a true null hypothesis.

In our example, we reject the null hypothesis if \(T<t_{\alpha/2,\,2n-2}\) (kit A lower) or \(T>t_{1-\alpha/2,\, 2n-2}\) (kit B lower). For \(\alpha=5\%\) and \(n=10\), these thresholds are \(t_{0.025,\,18}=\) -2.1 and \(t_{0.975,\,18}=\) 2.1, and our observed \(t\)-statistic lies within these thresholds; the hypothesis is not rejected.

All cautionary notes for \(p\)-values apply to significance statements as well. In particular, just because our test found a significant difference does not imply that the difference is practically meaningful:

Statistical significance does not imply scientific significance.

Moreover, the \(p\)-value or a statement of significance concern a single experiment, but an isolated significant result is not enough to establish scientific significance of a result. As R. A. Fisher rightly insisted:

In order to assert that a natural phenomenon is experimentally demonstrable we need, not an isolated record, but a reliable method of procedure. In relation to the test of significance, we may say that a phenomenon is experimentally demonstrable when we know how to conduct an experiment which will rarely fail to give us a statistically significant result. (Fisher 1971)

Error probabilities

Any statistical test has four possible outcomes under the significant / non-significant dichotomy, which we summarize in Table 2.4. A significant result leading to rejection of \(H_0\) is called a positive. If the null hypothesis is indeed false, then it is a true positive, but if the null hypothesis is indeed true, it was incorrectly rejected: a false positive or type-I error. The significance level \(\alpha\) is the probability of a false positive and by choosing a specific value, we can control the type-I error of our test. The specificity of the test is the probability \(1-\alpha\) that we do not reject a true null hypothesis.

Conversely, a non-significant result is called a negative. Not rejecting a true null hypothesis is a true negative, incorrectly not rejecting a false null hypothesis is a false negative or a type-II error. The probability of a false negative test outcome is denoted by \(\beta\). The power or sensitivity of the test is the probability \(1-\beta\) that we correctly reject the null hypothesis. The larger the true effect size, the more power a test has to detect it. Power analysis allows us to determine the test parameters (most importantly, the sample size) to provide sufficient statistical power to detect an effect size that is deemed scientifically relevant.

Table 2.4: The four possible outcomes of a hypothesis test.

	\(H_0\) true	\(H_0\) false
No rejection	true negative (TN)	false negative (FN)
	specificity \(1-\alpha\)	\(\beta\)
Rejection	false positive (FP)	true positive (TP)
	\(\alpha\)	sensitivity or power \(1-\beta\)

Everything else being equal, the two error probabilities \(\alpha\) and \(\beta\) are adversaries: by lowering the significance level \(\alpha\), larger effects are required to reject the null hypothesis, which simultaneously increases the probability \(\beta\) of a false negative.

This has an important consequence: if our experiment has low power (it is underpowered), then only large effect sizes yield statistical significance. A significant \(p\)-value and a large effect size then tempt us to conclude that we reliably detected a substantial difference, even though we must expect such as result with probability \(\alpha\) in the case that no difference exists.

Under repeated application of a test with new data, then \(\alpha\) and \(\beta\) are the expected frequencies—the false positive rate respectively the false negative rate—of the two types of error. This interpretation is helpful in scenarios such as quality control. On the other hand, we usually conduct only a limited number of repeated test in scientific experimentation. Here, we can interpret \(\alpha\) and \(\beta\) as quantifying the severity of a statistical test—its hypothetical capability to detect a desired difference in a planned experiment. This is helpful for planning experiments to ensure that the data generated will likely provide sufficient evidence against an incorrect scientific hypothesis.

Rejection regions and confidence intervals

Instead of rejecting \(H_0\) if the test statistic \(T\) exceeds the respective \(t\)-quantiles, we can also determine the corresponding limits on the estimated difference \(\hat{\Delta}\) directly and reject if \[\begin{equation} \hat{\Delta}> t_{1-\alpha/2,\,2n-2}\cdot\sqrt{2}\cdot \hat{\sigma}/\sqrt{n} \quad\text{or}\quad \hat{\Delta}< t_{\alpha/2,\,2n-2}\cdot\sqrt{2}\cdot \hat{\sigma}/\sqrt{n} \tag{2.2} \;. \end{equation}\] The corresponding set of values is called the rejection region \(\mathcal{R}\) and we reject \(H_0\) whenever the observed difference \(\hat{\Delta}\) is inside \(\mathcal{R}\). In our example, \(\mathcal{R}\) consists of the two sets \((-\infty,\) -1.06 \()\) and \((\) 1.06 \(, +\infty)\). Since \(\hat{\Delta}=\) -0.34 does not fall into this region, we do not reject the null hypothesis.

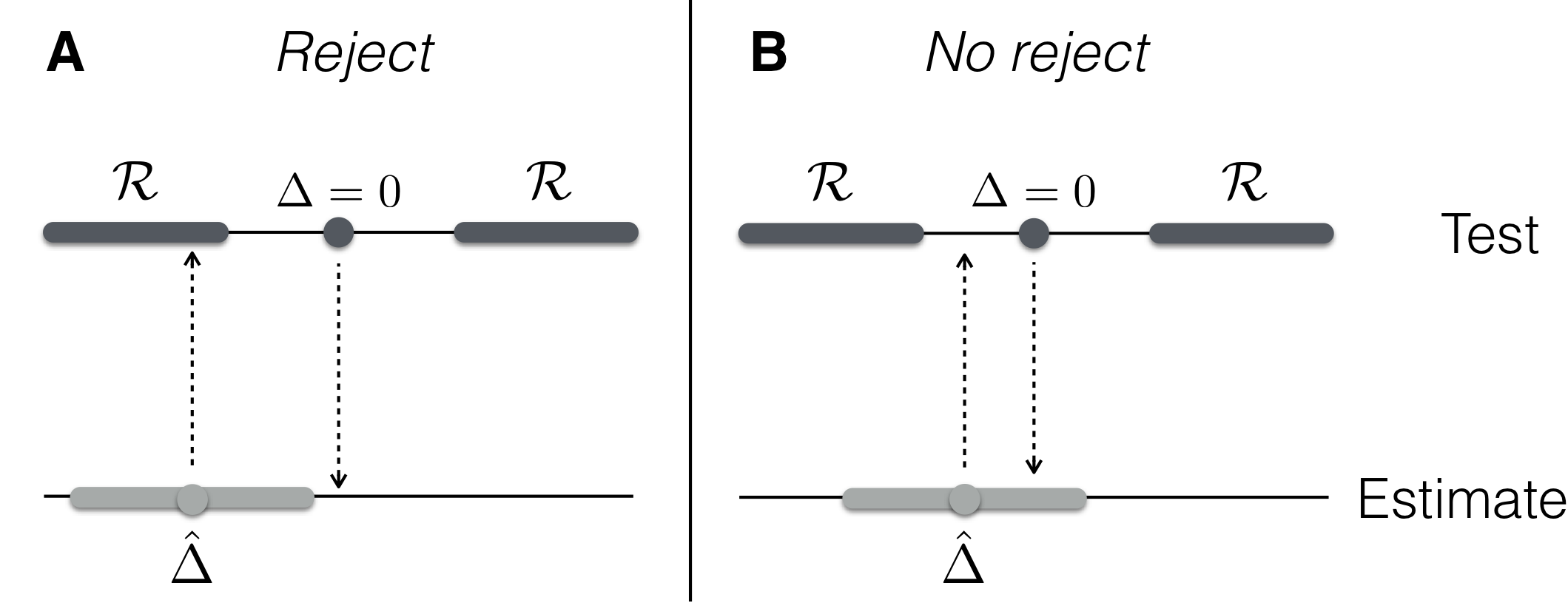
Figure 2.9: Illustrating equivalence of testing and estimation. Left: estimate is in rejection region and null value is outside the confidence interval. Right: estimate outside rejection region, confidence interval contains null value. Top: null value (dark grey dots) and rejection region (dark grey shade); bottom: estimate \(\hat{\Delta}\) (light grey dots) and confidence interval (light grey shade).

There is a one-to-one correspondence between the rejection region \(\mathcal{R}\) for a significance level \(\alpha\), and the \((1-\alpha)\)-confidence interval of the estimated difference. The estimated effect \(\hat{\Delta}\) lies inside the rejection region if and only the value 0 lies outside its \((1-\alpha)\)-confidence interval. This equivalence is illustrated in Figure 2.9. In hypothesis testing, we put ourselves on the value under \(H_0\) (e.g., \(\Delta=0\)) and check if the estimated value \(\hat{\Delta}\) is so far away that it falls inside the rejection region. In estimation, we put ourselves at the estimated value \(\hat{\Delta}\) and check if the data provide no objection against the hypothesized value under \(H_0\), which then falls inside the confidence interval. Our previous argument that the 95%-confidence interval of \(\hat{\Delta}\) does contain zero is therefore equivalent with our current result that \(H_0: \Delta=0\) cannot be rejected at the 5%-significance level.

2.3.4 Three additional test statistics

We briefly present three more significance test statistics for testing expectations and for testing variances. Their distributions under the null hypothesis are all based on normally distributed data.

\(z\)-test of mean difference

The \(t\)-test of the hypothesis \(H_0: \Delta=0\) is exact and considers the additional uncertainty in the distribution of the test statistic \(T\) that we introduce by using an estimate \(\hat{\sigma}\) of the standard deviation. For large sample sizes \(n\), the \(t\)-distribution with \(n\) degrees of freedom quickly approaches a standard normal distribution. If \(2n-2\) is “large enough” (typically, \(n>20\) suffices), we can compare the test statistic \[ T = \frac{\hat{\Delta}}{\widehat{\text{se}}(\hat{\Delta})} = \frac{\hat{\mu}_A-\hat{\mu}_B}{2\hat{\sigma}/\sqrt{n}} \] with the quantiles \(z_\alpha\) of the standard normal distribution, and reject \(H_0\) is \(T>z_{1-\alpha/2}\) or \(T<z_{\alpha/2}\). This test is sometimes called a \(z\)-test and yields results indistinguishable from the \(t\)-test for large samples sizes. Since both the \(t\)- and the \(z\)-test are equally easy to perform using a computer, however there is usually no reason to forego the exactness of the \(t\)-test.

For our example, we reject the null-hypothesis at a 5%-level if the test statistic \(T\) is below \(z_{\alpha/2}=\) -1.96 respectively above \(z_{1-\alpha/2}=\) 1.96, as compared to the thresholds \(t_{\alpha/2,2n-2}=\) -2.02 and \(t_{1-\alpha/2,2n-2}=\) 2.02.

\(\chi^2\)-test of variance

Given an estimate \(\hat{\sigma}^2\) from normally distributed observations based on \(d\) degrees of freedom , we can use a \(\chi^2\)-test to test if the true variance is equal to a specific value \(\sigma_0^2\). Under the null-hypothesis \(H_0:\sigma^2=\sigma_0^2\), the test statistic \[ T = \frac{d\cdot\hat{\sigma}^2}{\sigma_0^2} \] has a \(\chi^2\)-distribution with \(d\) degrees of freedom. We reject \(H_0\) if \(T<\chi^2_{\alpha/2,d}\) or \(T>\chi^2_{1-\alpha/2,d}\). It is sometimes sufficient to test if the true variance is smaller than \(\sigma_0^2\) such that we establish an upper bound for the variance. We reject this hypothesis if \(T>\chi^2_{1-\alpha,d}\) (note that we use \(\alpha\) here and not \(\alpha/2\)), but the true variance can be arbitrarily smaller than \(\sigma_0^2\) if we do not reject the null-hypothesis.

For our example data for vendor A, we have \(n=\) r normally distributed samples and the variance estimate is based on \(n-1=\) 9 degrees of freedom. We reject the hypothesis \(H_0:\sigma_A^2=3\) at a 5%-level if \(T=9\hat{\sigma}_A^2/3<\) 2.7 or \(T>\) 19.02. We calculate \(t=\) 11.31 and find a \(p\)-value of 0.75.

\(F\)-test of variance ratio

If we have two variance estimates \(\hat{\sigma}_A^2\) and \(\hat{\sigma}_B^2\), calculated from normally distributed samples and based on \(d_A\) and \(d_B\) degrees of freedom, respectively, we can test their equality using the test statistic \[ T = \frac{\hat{\sigma}_A^2}{\hat{\sigma}_B^2}\;. \] Under the null-hypothesis \(H_0:\sigma_A^2=\sigma_B^2\), which is equivalent to \(H_0:\sigma_A^2/\sigma_B^2=1\), the test statistic has an \(F\)-distribution with \(d_A\) numerator and \(d_B\) denominator degrees of freedom. We reject \(H_0\) if \(T<F_{\alpha/2,d_A,d_B}\) or \(T>F_{1-\alpha/2,d_A,d_B}\).

In our example, we have \(\hat{\sigma}_A^2=\) 3.77 and \(\hat{\sigma}_B^2=\) 1.69 based on \(d_A=d_B=n-1=\) 9 degrees of freedom each. This leads to a test statistic of \(T=\) 2.23. The critical values at a 5%-level are \(F_{0.025,9,9}=\) 0.25 and \(F_{0.975,9,9}=\) 4.03 and the resulting \(p\)-value is 0.25.

References

Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences. 2nd ed. Lawrence Erlbaum Associates, Hillsdale.

Fisher, R. 1956. Statistical Methods and Scientific Inference. 1st ed. Hafner Publishing Company, New York.

Fisher, R. 1971. The Design of Experiments. 8th ed. Hafner Publishing Company, New York.

Hedges, L., and I. Olkin. 1985. Statistical methods for meta-analysis. New York: Academic Press.

Nakagawa, Shinichi, and Innes C Cuthill. 2007. “Effect size, confidence interval and statistical significance: a practical guide for biologists.” Biol Rev Camb Philos Soc 82 (4). itchyshin@yahoo.co.nz: 591–605. https://doi.org/10.1111/j.1469-185X.2007.00027.x.

Popper, K R. 1959. The Logic of Scientific Discovery. Routledge.