Chapter 8 Split-unit designs

8.1 Introduction

In previous designs, we randomized all treatment factors on the same unit factor and these designs therefore have a single experimental unit factor. In some experimental setups, however, some treatment factors are easier to change than others or are easier applied to groups of units, while other treatment factors can easily be allocated to individual units.

For example, we might study the growth rate of a bacterium for different concentrations of glucose at different temperatures. Using 96-well plates for growing the bacteria, we can use a different amount of glucose for each well, but we are restricted to use the same temperature for the whole plate. In other words, a well is the experimental unit for the glucose treatment while a plate is the experimental unit for the temperature treatment.

This kind of design is known as a split-unit (or split-plot) design, where (at least) two treatment factors (glucose concentration and temperature) are randomized on different nested unit factors (plates and wells nested in plates). The precision of a contrast estimate then depends on the treatment factors involved and their respective experimental units.

A related experimental design is the criss-cross design (commonly called split-block or strip-plot), where the two experimental unit factors are crossed rather than nested. This design naturally arises, e.g., when using a multi-channel pipette in a 96-well experiment: with one treatment per channel, all columns in a row of the plate contain the same treatment. Using different concentrations for a dilution series randomized over columns yields the second treatment and experimental unit since all rows in a column use the same dilution.

Both types of designs require care in the model specification to correctly reflect the relations between treatments and units. Otherwise, precision and power are vastly overstated for some contrasts, resulting in deceptively low uncertainties and erroneous conclusions.

8.2 Simple split-unit design

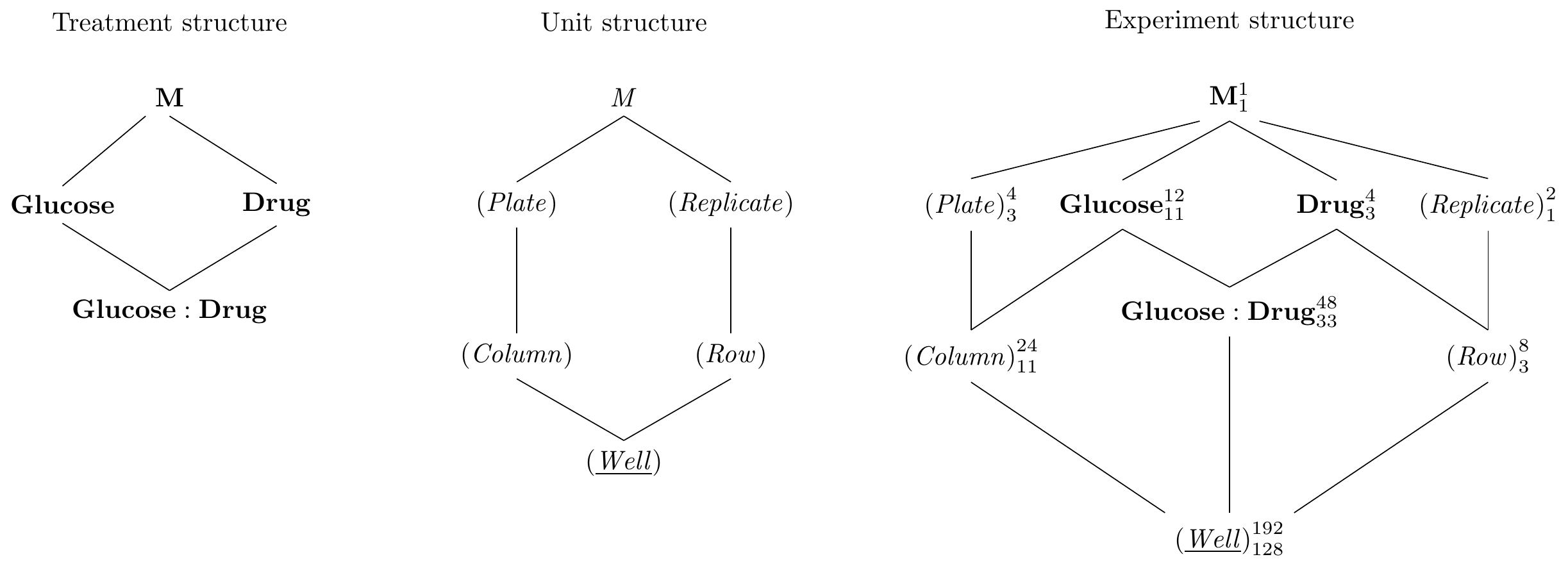
We begin our discussion using two nested unit factors and two crossed treatment factors. A common application of the split-unit design is the accommodation of hard-to-change factors. The idea is simple: applying a different level of one treatment factor is much more cumbersome than applying a different level of the other. To avoid frequent simultaneous changes of both levels, we keep the first treatment factor constant for a group of units, and only then randomize the second treatment factor within this group. This sacrifices precision and power for main effects of the whole-unit factor for the benefit of easier implementation. We call the first treatment factor the whole-unit treatment, and the group unit factor the whole-unit factor. We randomize the second treatment factor (the sub-unit treatment) on the ‘lower’ unit factor (the sub-unit factor).

8.2.1 Experiment

We revisit out drug-diet example, with three drugs (placebo, \(D1\), \(D2\)) combined with two diets (low-fat, high-fat) in an experiment with four mice per treatment, 24 mice in total, using enzyme level as our response.

In previous instances, we randomly assigned a drug-diet combination to each mouse (or each mouse in each block). To implement such an experiment, we have to individually apply the assigned drug to each mouse once at the beginning of the experiment. But we also have to feed each mouse its respective diet throughout the experiment; even if we hold several mice in one cage, we cannot apply the same diet to the whole cage, but have to individually feed each mouse within each cage.

A more practical implementation of the experiment uses eight cages with three mice, but while each mouse per cage is treated with a different drug, all mice in the same cage are fed the same diet. This makes each cage a block for the drugs, but the experimental unit for the diets. The experimental layout is shown in Figure 8.1.

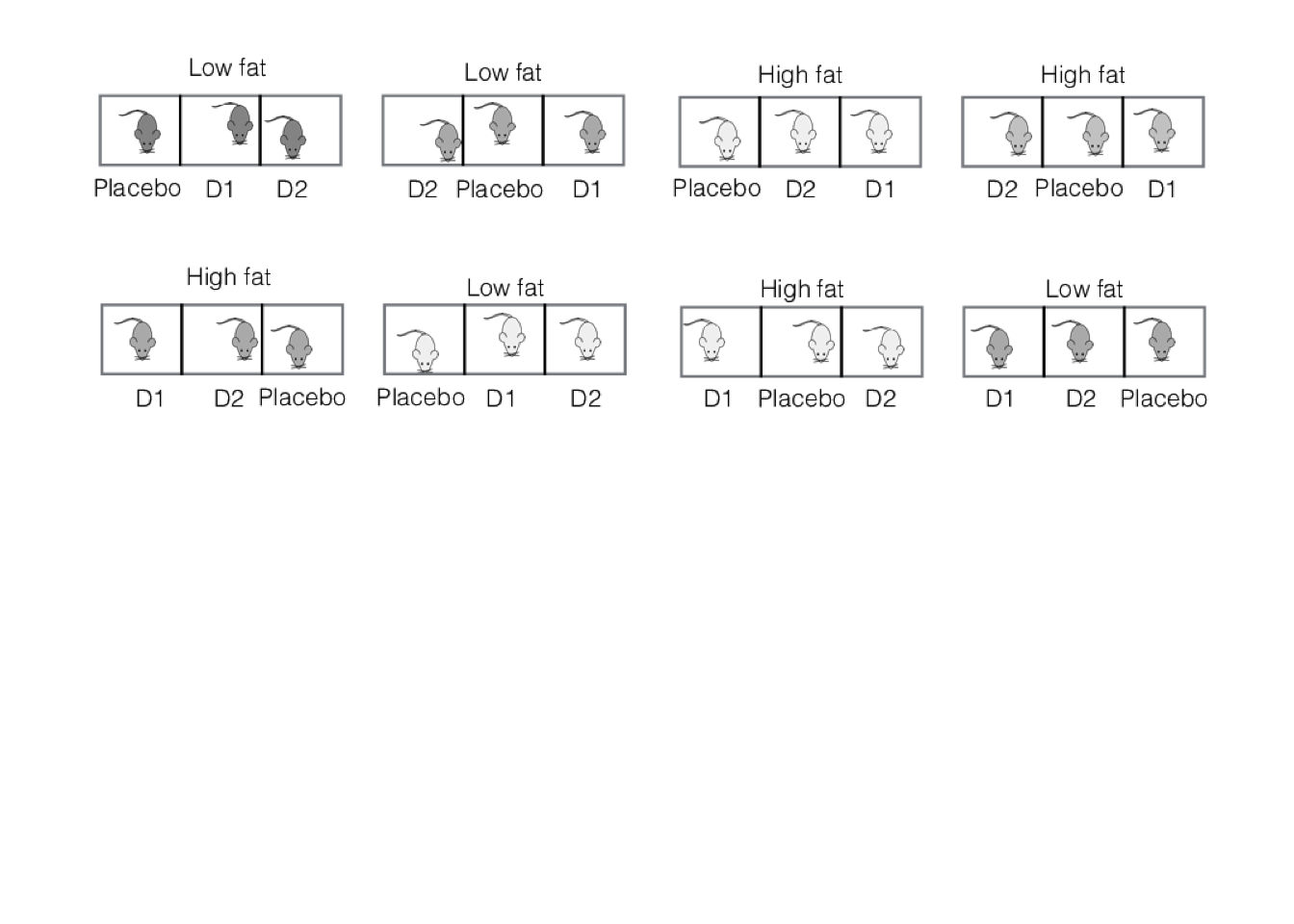
Split-unit experiment with two diets randomized on cages of three mice, and three drugs randomized on mice within cages.

Figure 8.1: Split-unit experiment with two diets randomized on cages of three mice, and three drugs randomized on mice within cages.

8.2.2 Hasse diagram

The Hasse diagrams are constructed using our previous approaches and are shown in Figure 8.2. The unit structure consists of the random factor (Mouse) (quite literally) nested in the random factor (Cage); since we measure one sample per mouse, (Mouse) is the response unit. The treatment structure is a \(3\times 2\) factorial with interaction.

In contrast to previous designs, the two treatment factors now have different experimental units: we feed all mice in a cage the same diet, and Diet is randomized on (Cage), indicated by drawing a line between them. Meanwhile, Drug is randomized on (Mouse). Moreover, each level of the interaction Diet:Drug is a combination of diet and drug. Since each cage only has one diet, these levels are assigned to mice, and we draw a corresponding line. No edge from Drug to (Mouse) is required, since it is implicit in the nesting of (Mouse) in Diet:Drug in Drug. As for most blocked designs, we assume that interactions between unit and treatment factors are negligible and do not include the factors (Cage:Drug) and (Cage:Diet:Drug).

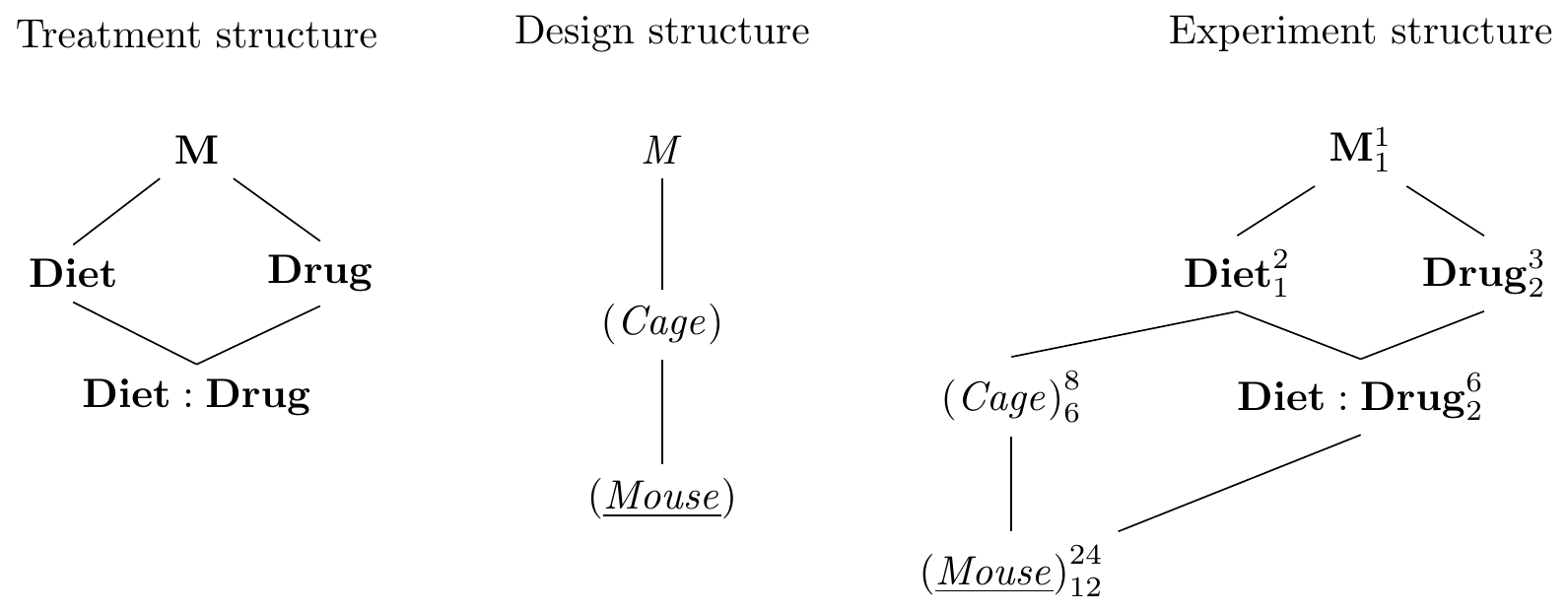
Split-unit design with diets randomized on cages and drugs randomized on mice within cages. Cages are a blocks for the drug treatment, but experimental units for the diet treatment.

Figure 8.2: Split-unit design with diets randomized on cages and drugs randomized on mice within cages. Cages are a blocks for the drug treatment, but experimental units for the diet treatment.

The experiment design diagram shows that (Cage) is a blocking factor for Drug (and Drug:Diet); this removes the between-cage variation for contrasts of drug main effects and drug-diet interactions, but not for contrasts involving only Diet. Likewise, the presence of more than one mouse per cage looks like pseudo-replication for diet main effects, and increasing the number of mice per cage does not increase replication for Diet.

The \(F\)-test and contrasts for Diet are based on the degrees of freedom and the variation associated with (Cage). Power and precision are therefore lower than for Drug and Drug:Diet, whose \(F\)-tests and contrasts are based on (Mouse). The loss of precision for the whole-unit factor is the principal disadvantage of a split-unit design. For our purposes, the design is still successful: first, it achieves the desired simplified implementation of the experiment. Second, our main research question concerns the effects of the three drugs (the Drug main effect) and their modification by the diet (the Drug:Diet interaction), and both are based on the full replication and the lowest residual variance terms in the design. We are not interested in comparing only the diets themselves and our intended analysis is therefore largely unaffected by the comparatively low replication and precision for the Diet main effect.

The linear model for this design is \[ y_{ijk} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + c_{jk} + e_{ijk}\;, \] where \(\alpha_i\), \(\beta_j\), \((\alpha\beta)_{ij}\) are the drug and diet main effect parameters, and the interaction parameters with \(i=1\dots 3\) and \(j=1\dots 2\). The random effect \(c_{jk}\sim N(0,\sigma_c^2)\) is effect for the eight cages, with \(k=1\dots 4\), and \(e_{ijk}\sim N(0,\sigma_e^2)\) are the residuals within each cage.

8.2.3 Analysis of variance

We derive the model specification directly from the experiment design diagram (Fig. 8.2). All random factors are present in the unit structure, and the Error() term is therefore Error(cage/mouse) or simply Error(cage). The fixed factors are all in the treatment structure, which is specified as drug*diet. The model specification is hence y~drug*diet+Error(cage), leading to the following ANOVA table with two error strata

## 
## Error: cage
##           Df Sum Sq Mean Sq F value Pr(>F)
## diet       1  4.501   4.501   2.005  0.207
## Residuals  6 13.467   2.244               
## 
## Error: Within
##           Df Sum Sq Mean Sq F value   Pr(>F)    
## drug       2  47.11  23.555  26.169 4.21e-05 ***
## drug:diet  2  11.20   5.599   6.221    0.014 *  
## Residuals 12  10.80   0.900                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Comparing the degrees of freedom in this table with those from the diagram confirms that our model specification corresponds to the design. We find each treatment factor exclusively in the error stratum of its experimental unit: Diet appears in the (Cage) error stratum and Drug and the interaction appear in the residual (Mouse) error stratum. The correct denominator for each \(F\)-test is found by starting from the corresponding treatment factor in the diagram, and following the edges downward until we find the first random factor: Diet is tested against the variation from cage to cage alone, and the \(F\)-test is based on one numerator and six denominator degrees of freedom. Since cage-to-cage variation also seems to be the dominant source of random variation in this experiment, we are unable to detect any significant main effect for Diet. On the other hand, both Drug and Drug:Diet are tested against the within-cage variation on twelve degrees of freedom. This variation has smaller mean squares and the resulting two \(F\)-tests have more power.

8.2.4 Analysis with linear mixed model

An equivalent analysis using the linear mixed model uses the specification y~drug*diet+(1|cage), where we directly find a between-cage variance of \(\hat{\sigma}_c^2=\) 0.45, which is about half of the residual variance \(\hat{\sigma}_e^2=\) 0.9, leading to an intra-class correlation of ICC=33%. In contrast to using litters, the cages provide a less efficient blocking factor. This is unproblematic, since we primarily introduced this factor as the experimental unit for the diet to simplify the experiment implementation, and take the reduction in variance for the drug effects as a welcome benefit.

The differences between the classical ANOVA and the modern linear mixed model approach lead to a different calculation of the sums of squares for Diet and (Cage). Since our design is fully balanced, the resulting \(F\)-values and \(p\)-values are nevertheless identical to those from the aov() result:

Type III Analysis of Variance Table with Kenward-Roger’s method
  Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
drug 47.11 23.55 2 12 26.17 4.21e-05
diet 1.805 1.805 1 6 2.005 0.2065
drug:diet 11.2 5.599 2 12 6.221 0.01401

The resulting \(F\)-test for the interaction term is again statistically significant and explains about 19% of the variation.

8.2.5 Contrast analysis

We define and estimate linear contrasts based on a split-unit design in the same way as before, and can rely on emmeans() for providing the required treatment group means. Owing to the two different experimental units in this design, however, contrasts of treatment groups of the same diet are more precise than those of groups with different diets. We see this from the Hasse diagram: if only one level of Diet is involved, we are essentially working with a blocked design and profit from intra-block comparisons of the drugs. Contrasts involving different diets require inter-block comparisons as well and suffer from lower replication and higher variance.

As an illustration, we first compare \(D1\) and \(D2\) to the placebo treatment separately under both diets. Using emmeans(), this can be conveniently done by specifying the formulae ~drug|diet for estimating the marginal means. Using a Dunnett-correction for multiple testing against a common reference level, our results confirm those from previous experiments: \(D1\) yields higher enzyme levels than placebo under both diets, while \(D2\) shows higher levels under a low-fat diet, but levels comparable to the placebo group for a high-fat diet.

Contrast diet Estimate SE df LCL UCL
D1 - Placebo low fat 2.66 0.67 12 0.97 4.35
D2 - Placebo low fat 3.22 0.67 12 1.53 4.91
D1 - Placebo high fat 4.07 0.67 12 2.38 5.77
D2 - Placebo high fat 1.30 0.67 12 -0.39 2.99

These four contrasts only compare treatment group means within the same diet. However, precision decreases for contrasts that involve comparisons between diets, such as contrasting the placebo averages between the two diets:

Contrast Estimate SE df LCL UCL
Placebo (high) - Placebo (low) -0.7 0.82 14.74 -2.45 1.06

While this contrast has equal precision than the four other contrasts in our previous completely randomized design and randomized complete block design, its estimate has higher standard error and lower precision in this split-unit design.

8.2.6 Inadvertent split-unit designs

The fact that several experimental unit factors are present requires particular care in setting up the analysis, and split-unit experiments are notorious for the many ways they can be incorrectly designed, analyzed, and interpreted. One problem is mis-specification of the model. Starting from the Hasse diagram, this problem is easily avoided and the results can be checked by comparing the degrees of freedom between diagram and ANOVA table.

A far more common problem is the inadvertent split-unit design, in which an experiment is intended as a completely randomized design (or any other design with a single experimental unit factor), but is then implemented as a split-unit design. Examples of such inadvertent split-unit designs are numerous in the literature, particularly (but by no means exclusively) in the engineering literature on process optimization and quality control.

Inadvertent split-unit designs often occur in the design phase when treatments are randomized on their experimental units and the design table is constructed. They also frequently occur in the implementation phase, when the person running the experiment deviates from the design table for a more convenient implementation. For example, we might design the drug-diet experiment as a CRD, but the technicians realize that lots of work can be saved by feeding the same diet to all mice in a cage. While this might seem like an innocent small change of the experimental plan to the technician, it effectively makes a split-unit design out of an anticipated CRD.

8.3 Variations

Once recognized, the split-unit design turns out to be quite ubiquitous in experimental work. We briefly discuss several variations of this design idea to explore its many additional uses: accommodating an additional factor in an already existing design, using more than two nested units and randomizing a treatment factor on each level of nesting, and covering experimental designs involving a (usually temporal) order of treatments and measurements such as for comparing a response before and after application of a treatment.

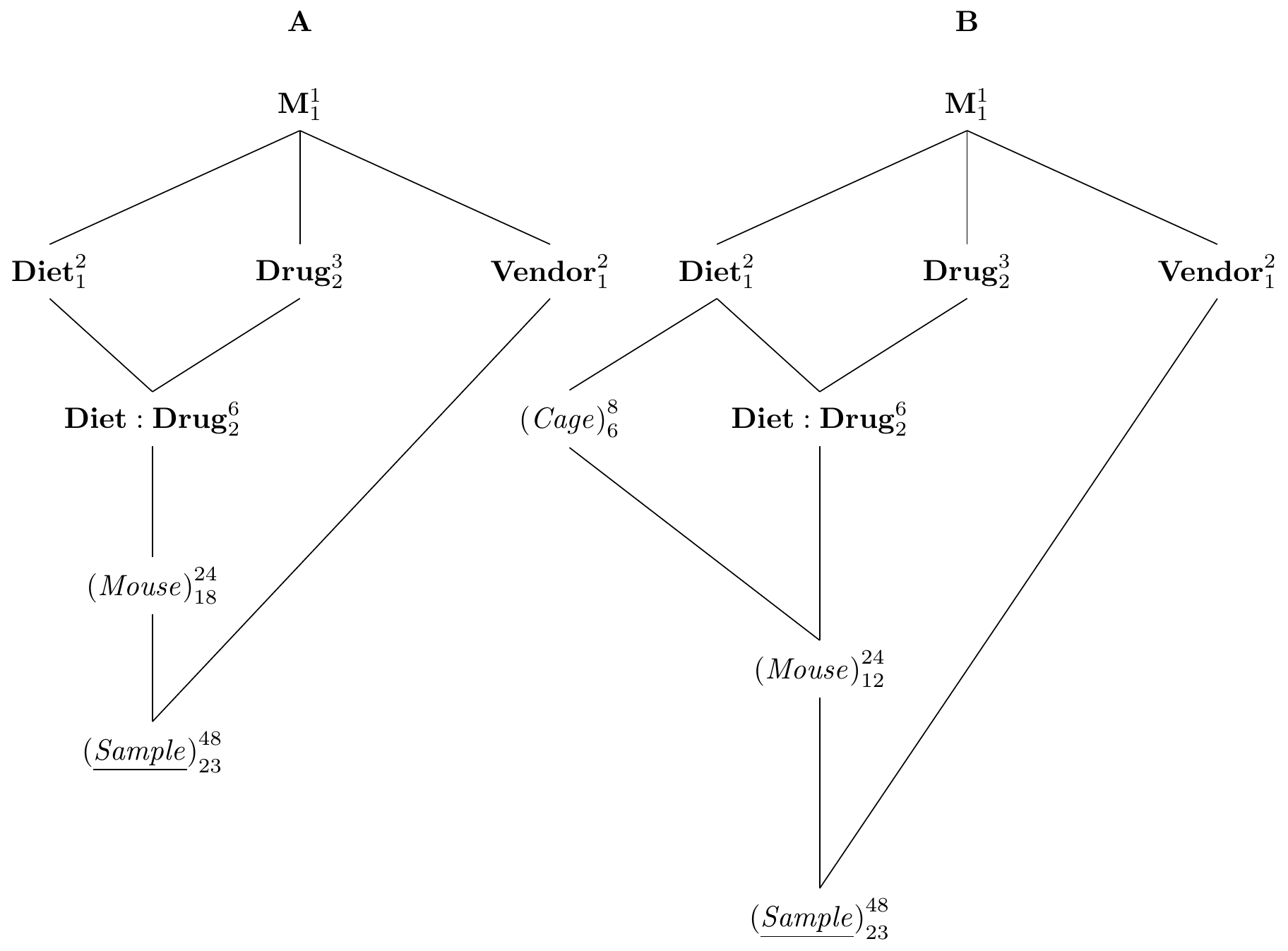
A: split-unit design with diets and drugs completely randomized on mice as a CRD and vendor randomized on samples. B: same treatment structure with split-split-unit design.

Figure 8.3: A: split-unit design with diets and drugs completely randomized on mice as a CRD and vendor randomized on samples. B: same treatment structure with split-split-unit design.

8.3.1 Accommodating an additional factor

We turned our previous drug-diet example into a split-unit design by grouping mice into cages and using the new grouping factor as experimental unit for the diets. This creates a whole-plot factor ‘above’ the original experimental unit. Similar to our discussion of choosing a blocking factor for an RCBD, we can alternatively sub-divide the original experimental unit further to create a sub-plot factor ‘below’.

To illustrate this idea, we consider the following situation: we start from our original drug-diet design with factorial treatment structure randomized on mice (a CRD). Previously, we also considered comparing two sample preparation kits from vendors A and B based on the enzyme level measurements. Since we already have our drug-diet experiment planned, we would like to ‘squeeze’ the comparison of the two kits into that experiment without jeopardizing our main objective of estimating contrasts of the drug-diet treatments.

The idea is simple: we draw two samples per mouse and randomly assigning kit A or kit B to each sample. The resulting experiment structure is the experiment shown in Figure 8.3A and we recognize it as a split-unit design. Here, the whole-plot unit (Mouse) is combined with a factorial treatment structure, and the sub-plot unit (Sample) is created nested in (Mouse) to compare levels of Vendor. The resulting treatment structure is a \(3\times 2\times 2\) factorial, where we removed all interactions involving Vendor under the assumption that these are negligible. This assumption is not crucial, but simplifies the design and interpretation considerably. The original drug-diet experiment is then unaffected by this augmentation of the design: even if vendor B’s kit is worse, we still have the full data for vendor A; simply removing the B data yields the data for the originally anticipated design.

We use the linear mixed model framework for estimating the corresponding model with specification y~drug*diet+vendor+(1|mouse) and estimating the difference between the two vendors.

Contrast Estimate SE df LCL UCL
Vendor A - Vendor B -0.4 0.18 23 -0.77 -0.02

This contrast is estimated very precisely with 23 residual degrees of freedom, the same as for a randomized complete block design with 24 mice as blocks and two samples per mouse and no other treatment factors. It has much higher precision than the drug or diet comparisons, because each mouse provides a block for Vendor to compare the two kits within each mouse.

8.3.2 Pretest-posttest designs

A common technique to increase precision is the pretest-posttest design, where the response variable is measured once before and once after the treatment is applied. This provides a simple way for adjusting the treatment response by a subject-specific baseline, and the difference between response after treatment and baseline is then considered as the relevant treatment effect. We consider a simple example of a pretest-posttest design with a single treatment factor, but the ideas readily extend to factorial treatment structures as well.

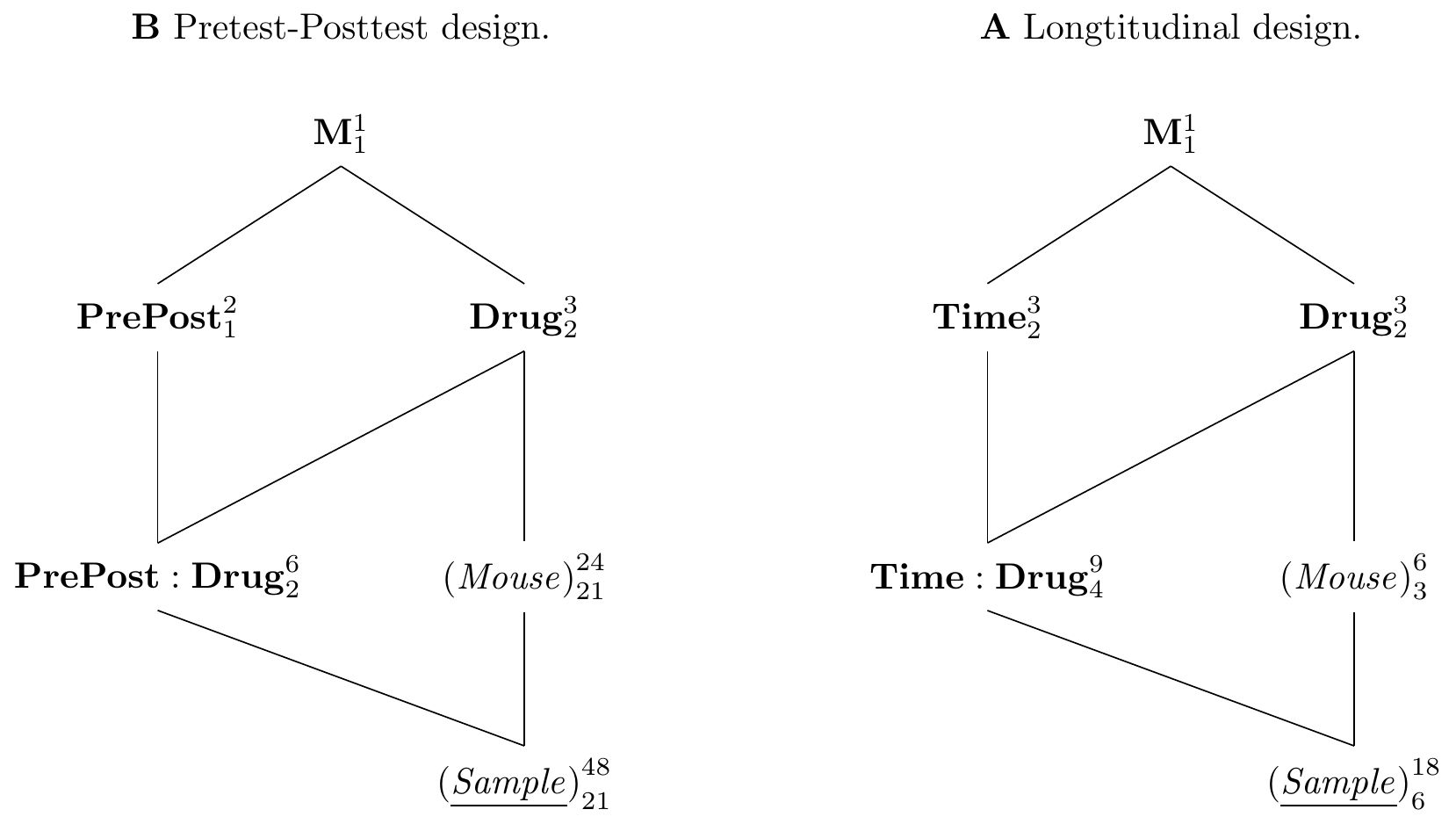
A: Pretest-posttest design with measurement before and after application of treatment to consider mouse-specific baseline response values. B: Longitudinal repeated measures design to allow multiple measurements of same mouse at different time-points.

Figure 8.4: A: Pretest-posttest design with measurement before and after application of treatment to consider mouse-specific baseline response values. B: Longitudinal repeated measures design to allow multiple measurements of same mouse at different time-points.

We consider our experiment for comparing three drugs, and use the baseline enzyme levels of each mouse in conjunction with the enzyme level after administration of the drug. The experiment diagram in Figure 8.4A illustrates this design. It contains two unit factors, (Sample) nested in (Mouse), since we take two samples from each mouse, one before, one after the drug administration. The design contains Drug as our main treatment factor, and we introduce PrePost with levels before and after as a second treatment factor. Both treatment factors are crossed and we introduce their interaction as a third treatment factor into the design. Since both samples belong to the same mouse, and a drug is applied to a mouse after the baseline measurement is taken, (Mouse) is the experimental unit for Drug and a block for PrePost. The corresponding models are y~prepost*drug+Error(mouse) for aov(), and y~prepost*drug+(1|mouse) for lmer().

There are three \(F\)-tests: the pre-post main effect compares the average response over all drugs, taken before the treatment is applied, to that taken after it is applied. We expect that the measured enzyme levels are not systematically different between the three drug groups before applying the treatment. Thus, a small and non-significant pre-post main effect either indicates that the before and after responses are identical for all drugs; none of the drugs has any discernible effect. Or it might be that one drug increases the enzyme level, and another drug decreases it, and the two effects cancel out.

The drug main effect \(F\)-test tests if the average enzyme levels are identical for all three drugs, when before and after measurements are lumped together. The denominator mean squares for this test stem from the mouse-to-mouse variation. This test is therefore the least powerful in this design, but also the least interesting.

Of greatest interest is usually the prepost-by-drug interaction, which shows how different the changes of enzyme levels from baseline to post-treatment measurement are between drugs. This is essentially the drug effect corrected for the baseline measurement. We can replicate the corresponding \(F\)-test as follows: for each mouse \(i\), calculate the difference \(\Delta_i=y_{i,\text{post}}-y_{i,\text{pre}}\) of the post-treatment response and the pre-treatment response. This ‘adjusts’ the response to the treatment by the baseline value. Now, we perform a one-way ANOVA with Drug as the treatment factor, and \(\Delta_i\) as the response variable. The resulting \(F\)-ratio and \(p\)-value are identical to the prepost-by-drug interaction in the pretest-posttest design.

8.3.3 Longitudinal design

Split-unit designs are sometimes still used for repeated measures and longitudinal designs, in which multiple response variables are measured for the same experimental unit, respectively the same response variable is measured at multiple occasions for the same experimental unit. Both designs thus have a more complex response structure than the classical approach can handle, and more appropriate models—including more complex variants of the linear mixed model—should be preferred.10

The use of split-unit designs for analyzing longitudinal or repeated measures data is rather a relict from pre-computer times when they were frequently used. Two main caveats of the classical approach are the assumption that any pair of time-points has the same correlation (but measurements closer in time tend typically have stronger correlations than those further apart) and using time as an ordinary treatment factor (but its levels cannot be randomized on units). Note that these caveats also apply to the pretest-posttest designs, but are unproblematic here because only two time-points are considered.

An example of a classical treatment of a longitudinal design is shown in Figure 8.4B, where three drugs are randomized on two mice each, and each mouse is then measured at three different time-points. In this design, we randomize Drug on (Mouse), which is a blocking factor for Time and the Time:Drug interaction. In other words, by measuring the same mouse at each time-point, we can relate the response values over time to get the profile from a single mouse. There is no need to compare average responses over time, since we can directly compare within each mouse. The mouse-to-mouse variation is then present when comparing the drug main effects, but is taken out of the comparisons involving Time.

8.4 A historical example

In 1935, John Yates published a soon to-be classic paper called “Complex Experiments” (Yates 1935), in which he reviews and expands the advances in statistical design of experiments since then 1920s. The paper contains an experiment to investigate different varieties of oat using different levels of nitrogen as fertilizer. We briefly discuss this experiment and its possible analyses to provide an additional example of a split-unit design. The experiment is shown in Figure 8.5: the three oat varieties “Victory”, “Golden Rain”, and “Marvellous” (denoted \(v_1,\dots,v_3\)) are applied to plots of sufficient size. Meanwhile, the four nitrogen levels \(n_j\) are applied to much smaller patches of land, denoted subplots (nested in plots) in this experiment. This yields a split-unit design with varieties randomized on plots, and nitrogen on subplots nested in plots. The whole experiment is replicated in six blocks, and 72 yields are recorded. The data are shown in Figure 8.5 individually for each block.11 Block effects are clearly visible, and patterns are very similar between blocks, so assuming no block-by-treatment interaction seems reasonable. We also observe a pronounced trend of increasing yield with increasing nitrogen level, and this trend seems roughly linear. Differences between oat varieties are less obvious.

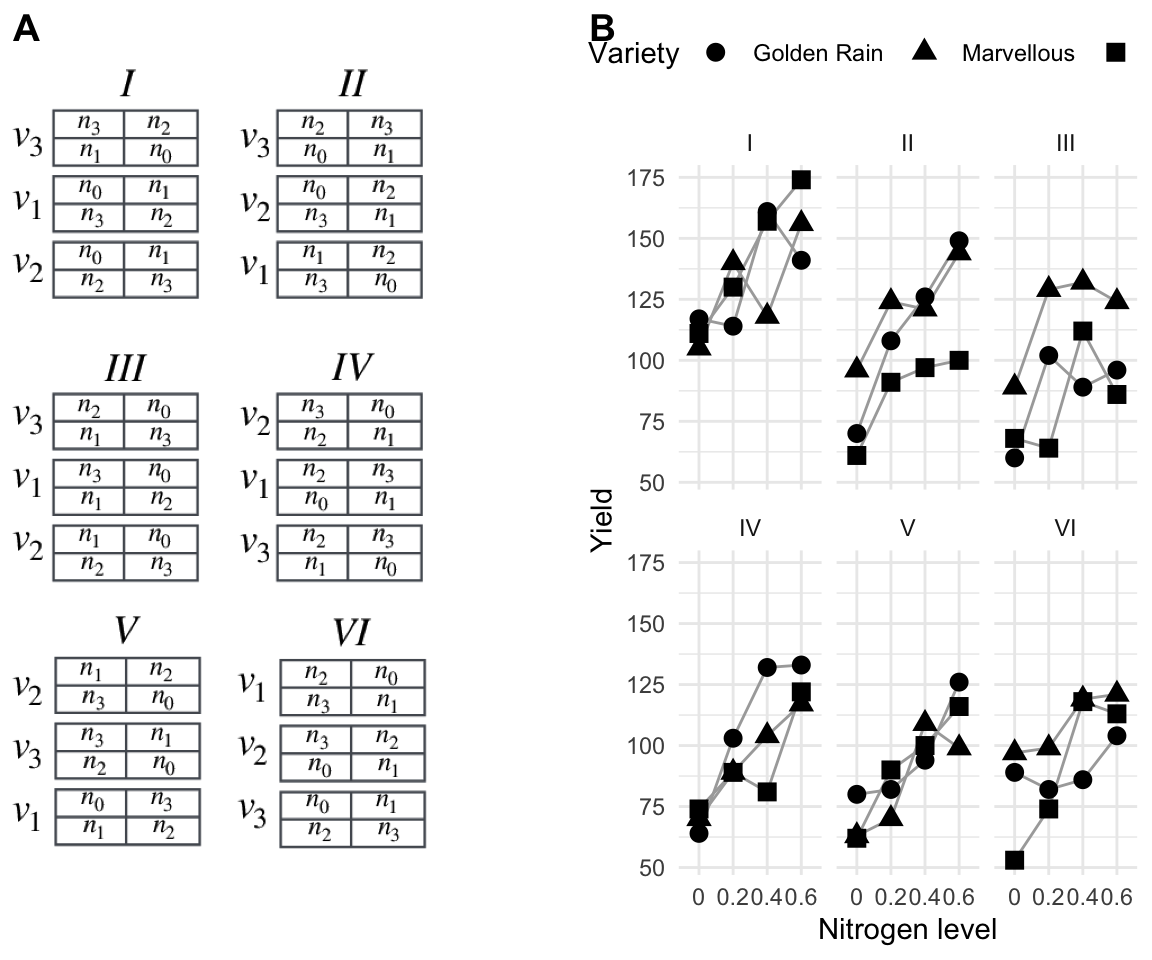
A: Classical experiment testing three varieties of oat and four levels of nitrogen in the fertilizer. Split-unit design with oat variety randomized on plots, nitrogen amount randomized on subplots within plots, and replication in six blocks. B: Data shown separately for each block, point shape indicates the oat variety.

Figure 8.5: A: Classical experiment testing three varieties of oat and four levels of nitrogen in the fertilizer. Split-unit design with oat variety randomized on plots, nitrogen amount randomized on subplots within plots, and replication in six blocks. B: Data shown separately for each block, point shape indicates the oat variety.

The Hasse diagrams are given in Figure 8.6 and show the simple factorial treatment structure and the chain of nested unit factors combined into a fairly complex design, where the whole treatment structure is blocked, and the nitrogen and interaction treatment factors are additionally blocked by the plots.

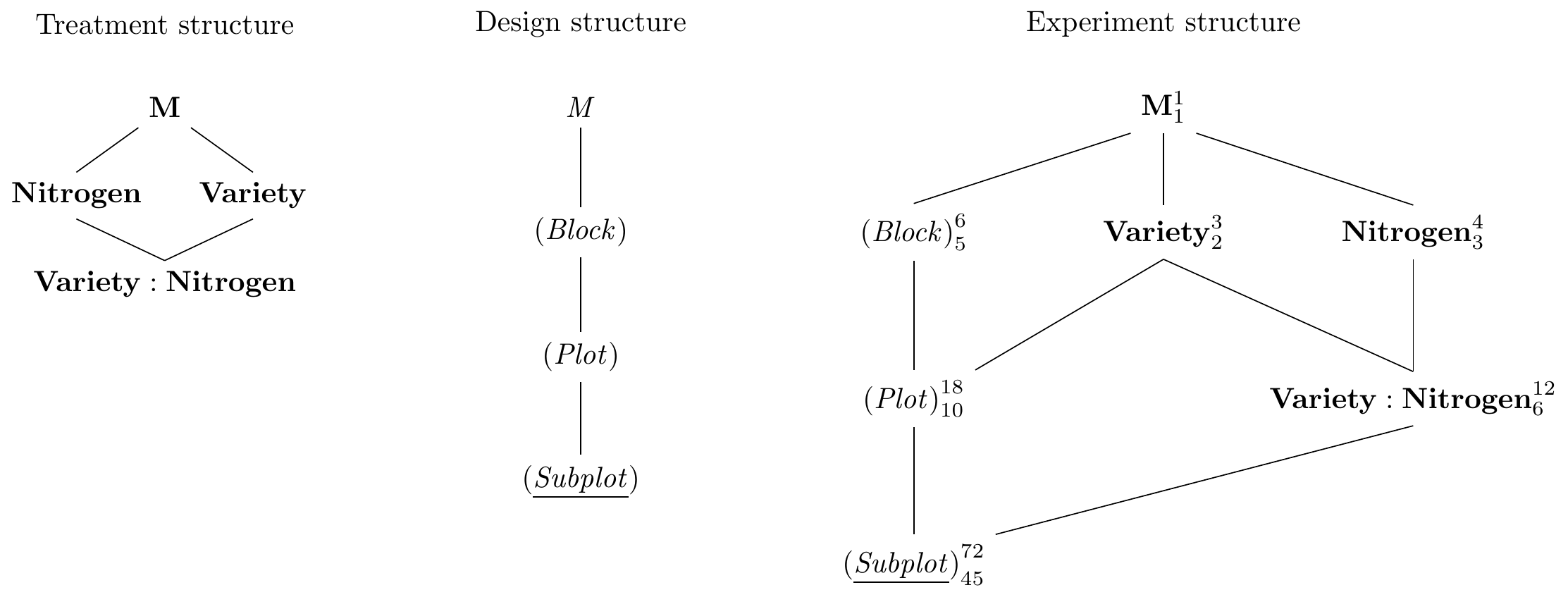
Hasse diagram for Yates' oat variety and nitrogen example with two treatment factors randomized on plots respectively subplots in plots, and replication in six blocks.

Figure 8.6: Hasse diagram for Yates’ oat variety and nitrogen example with two treatment factors randomized on plots respectively subplots in plots, and replication in six blocks.

The original analysis in 1930 was of course done using an analysis of variance approach. Here, we analyze the experiment using a linear mixed model and derive the specification Variety*nitro+(1|Block)+(1|Plot:Block) from the Hasse diagram. This yields the following ANOVA table:

Type III Analysis of Variance Table with Kenward-Roger’s method
  Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
Variety 526.1 263 2 10 1.485 0.2724
nitro 20021 6674 3 45 37.69 2.457e-12
Variety:nitro 321.7 53.62 6 45 0.3028 0.9322

The small and non-significant interaction shows that increasing the nitrogen level has roughly the same effect on yield for all three oat varieties. In addition, differences between oat varieties are also small with average yields between 80 and 175 and differences all less than 10, and not significant. The nitrogen level, on the other hand, shows a large and highly significant effect, and higher levels give more yield.

We further quantify these findings by estimating corresponding contrasts and their confidence intervals. First, we compare the varieties within each nitrogen level (Table 8.1). In each case, Marvellous provides higher yield than both Golden Rain and Victory, and Golden Rain gives higher yield than Victory: the varieties have a clear order, which is stable over all nitrogen levels. As the confidence intervals show, however, none of the differences are significant, and the precision of estimates is fairly low.

Table 8.1: Comparing the three varieties averaged within each level of fertilizer.
contrast nitro estimate SE df lower.CL upper.CL
0.0
Golden Rain - Marvellous 0 -6.67 9.71 30.23 -30.61 17.27
Golden Rain - Victory 0 8.50 9.71 30.23 -15.44 32.44
Marvellous - Victory 0 15.17 9.71 30.23 -8.77 39.11
0.2
Golden Rain - Marvellous 0.2 -10.00 9.71 30.23 -33.94 13.94
Golden Rain - Victory 0.2 8.83 9.71 30.23 -15.11 32.77
Marvellous - Victory 0.2 18.83 9.71 30.23 -5.11 42.77
0.4
Golden Rain - Marvellous 0.4 -2.50 9.71 30.23 -26.44 21.44
Golden Rain - Victory 0.4 3.83 9.71 30.23 -20.11 27.77
Marvellous - Victory 0.4 6.33 9.71 30.23 -17.61 30.27
0.6
Golden Rain - Marvellous 0.6 -2.00 9.71 30.23 -25.94 21.94
Golden Rain - Victory 0.6 6.33 9.71 30.23 -17.61 30.27
Marvellous - Victory 0.6 8.33 9.71 30.23 -15.61 32.27

For quantifying the dose-reponse relationship between nitrogen level and yield, we estimate the nitrogen main effect contrasts independently within each oat variety. We use a polynomial contrast for nitrogen, which provides information about linear, quadratic, and cubic components of a dose-response. The results are shown in Table 8.2.

Table 8.2: Orthogonal contrast analysis for nitrogen levels within each oat variety shows clear linear dose-reponse relation.
contrast Variety estimate SE df t.ratio p.value
Golden Rain
linear Golden Rain 150.67 24.30 45 6.20 0.00
quadratic Golden Rain -8.33 10.87 45 -0.77 0.45
cubic Golden Rain -3.67 24.30 45 -0.15 0.88
Marvellous
linear Marvellous 129.17 24.30 45 5.32 0.00
quadratic Marvellous -12.17 10.87 45 -1.12 0.27
cubic Marvellous 14.17 24.30 45 0.58 0.56
Victory
linear Victory 162.17 24.30 45 6.67 0.00
quadratic Victory -10.50 10.87 45 -0.97 0.34
cubic Victory -16.50 24.30 45 -0.68 0.50

For each variety, we find a substantial linear upward trend, with higher nitrogen levels providing higher yield. Since both quadratic and cubic terms are small and not significant, we can ignore all potential curvature in the trends and arrive at an easy to interpret result. We already determined that the average and nitrogen-level-specific yields are almost identical between varieties. The current contrasts additionally show that the estimates of the three linear components are all within one standard error of each other, demonstrating a comparable dose-response relation for all three varieties. This of course agrees with the previous result that there is no variety-by-nitrogen interaction.

References

Yates, F. 1935. “Complex Experiments.” Journal of the Royal Statistical Society 2 (2). Blackwell Publishing for the Royal Statistical Society: 181–247. https://doi.org/10.2307/2983638.

  1. For a comprehensive introduction to longitudinal analysis, see for example (Fitzmaurice, Laird, and Ware 2011), where our designs are discussed in chapter 5.↩

  2. The data are available in R from the nlme package with the command data(Oats, package = 'nlme').↩

  3. The availability of liquid-handling robots resulted in a new interest in these designs; see for example (Buzas, Wager, and Lansky 2011), which discuss split-unit and criss-cross designs in this context.↩